Задание
Правило
- Если в каждой точке \(\displaystyle x_0 \in (a;\,b)\) производная \(\displaystyle f^{\prime}(x_0)\) существует и \(\displaystyle f^{\prime}(x_0)>0{ \small ,}\)
то функция \(\displaystyle f(x)\) возрастает на интервале \(\displaystyle (a;\,b){\small .}\)
- Если в каждой точке \(\displaystyle x_0 \in (a;\,b)\) производная \(\displaystyle f^{\prime}(x_0)\) существует и \(\displaystyle f^{\prime}(x_0)<0{ \small ,}\)
то функция \(\displaystyle f(x)\) убывает на интервале \(\displaystyle (a;\,b){\small .}\)
Определение
Точки экстремума
Точки минимума и максимума называются точками экстремума.
Правило
Алгоритм нахождения точек экстремума дифференцируемой функции
- Находим производную функции и приравниваем к нулю.
- Находим точки, в которых производная равна нулю.
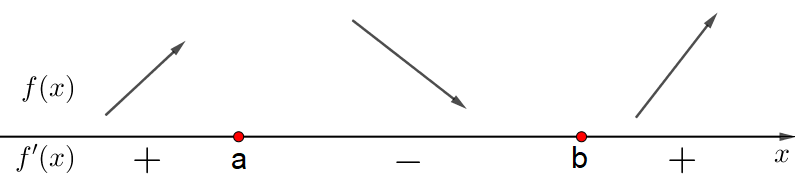
- Отмечаем корни производной на числовой прямой, а также определяем ее знаки на получившихся интервалах.
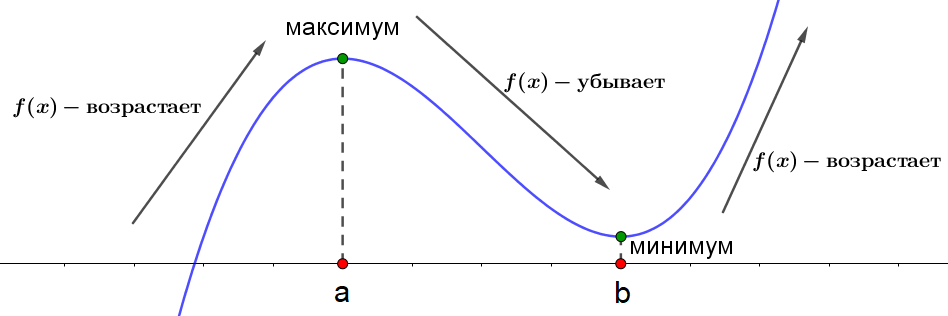
- Если производная меняет в найденной точке знак с \(\displaystyle +\) на \(\displaystyle -{\small ,}\)
то эта точка – точка максимума.
Если производная меняет в найденной точке знак с \(\displaystyle -\) на \(\displaystyle +{\small ,}\)
то эта точка – точка минимума.
Решение