Найдите значение выражения:
\(\displaystyle \frac{3\cos(\pi - \beta) + \sin\left(\dfrac{\pi}{2} + \beta\right)} { \cos(\beta + 3\pi)}=\)
Применим формулы приведения по правилу:
1) Определяем четверть, предполагая \(\displaystyle \alpha \in \left(0;\frac{\pi}{2}\right){\small .}\)
2) Определяем знак исходной функции.
3) Определяем, какая функция будет.
Если к углу \(\displaystyle \pm \alpha \) добавляем или вычитаем
- \(\displaystyle \pm\pi ,\, \pm 2\pi ,\, \pm 3\pi,\, \pm 4\pi,\,\ldots\) (целое число \(\displaystyle \pi\)), то функцию не меняем;
- \(\displaystyle \pm\frac{\pi}{2},\, \pm\frac{3\pi}{2},\, \pm\frac{5\pi}{2},\, \pm\frac{7\pi}{2},\, \ldots\) (нечетное число половинок \(\displaystyle \pi\)), то функцию меняем: \(\displaystyle \sin\) \(\displaystyle \leftrightarrow\) \(\displaystyle \cos\) и \(\displaystyle \tg\) \(\displaystyle \leftrightarrow\) \(\displaystyle \ctg{\small .}\)
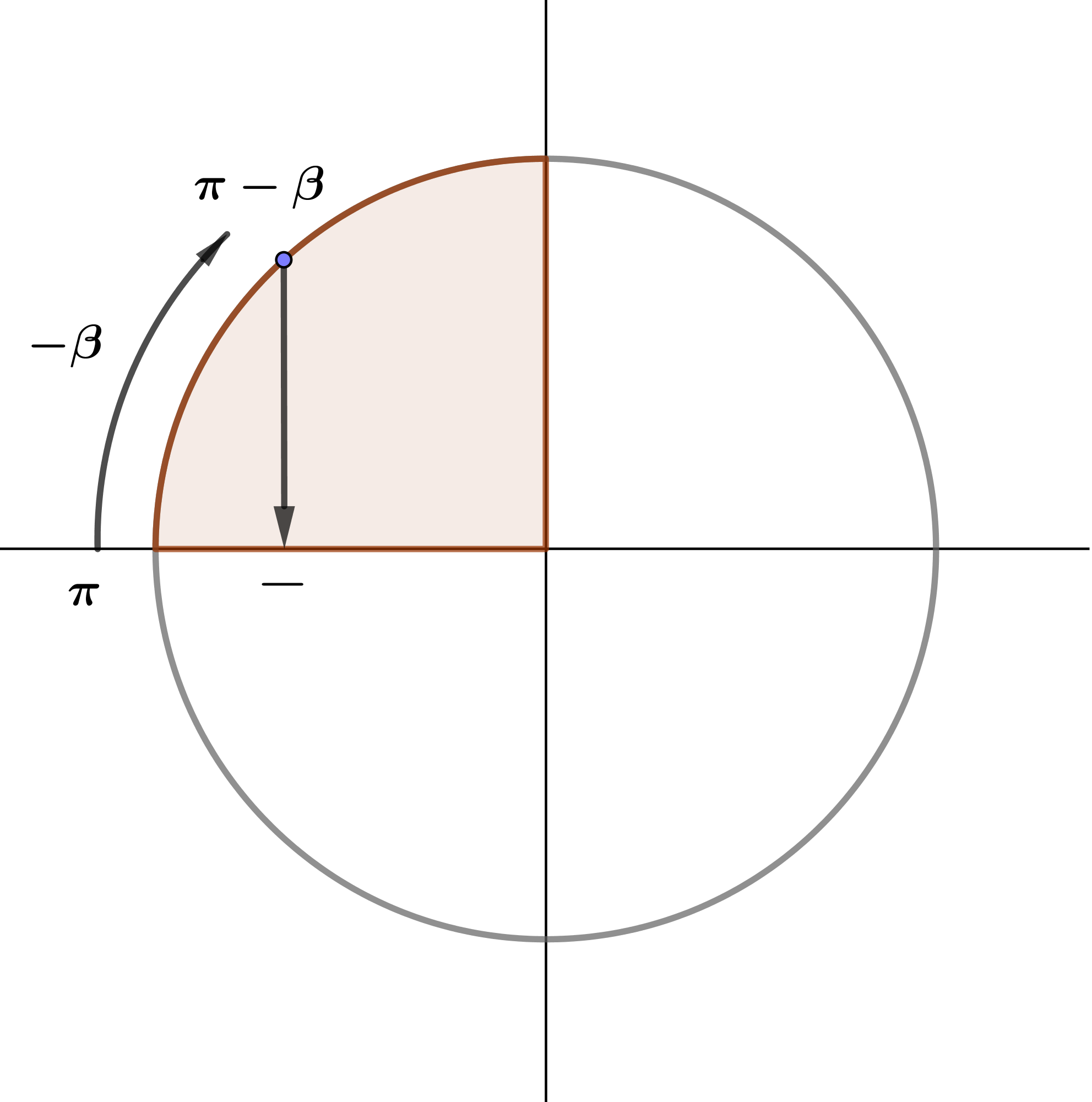
\(\displaystyle \cos(\pi - \beta)=-\cos\beta \)
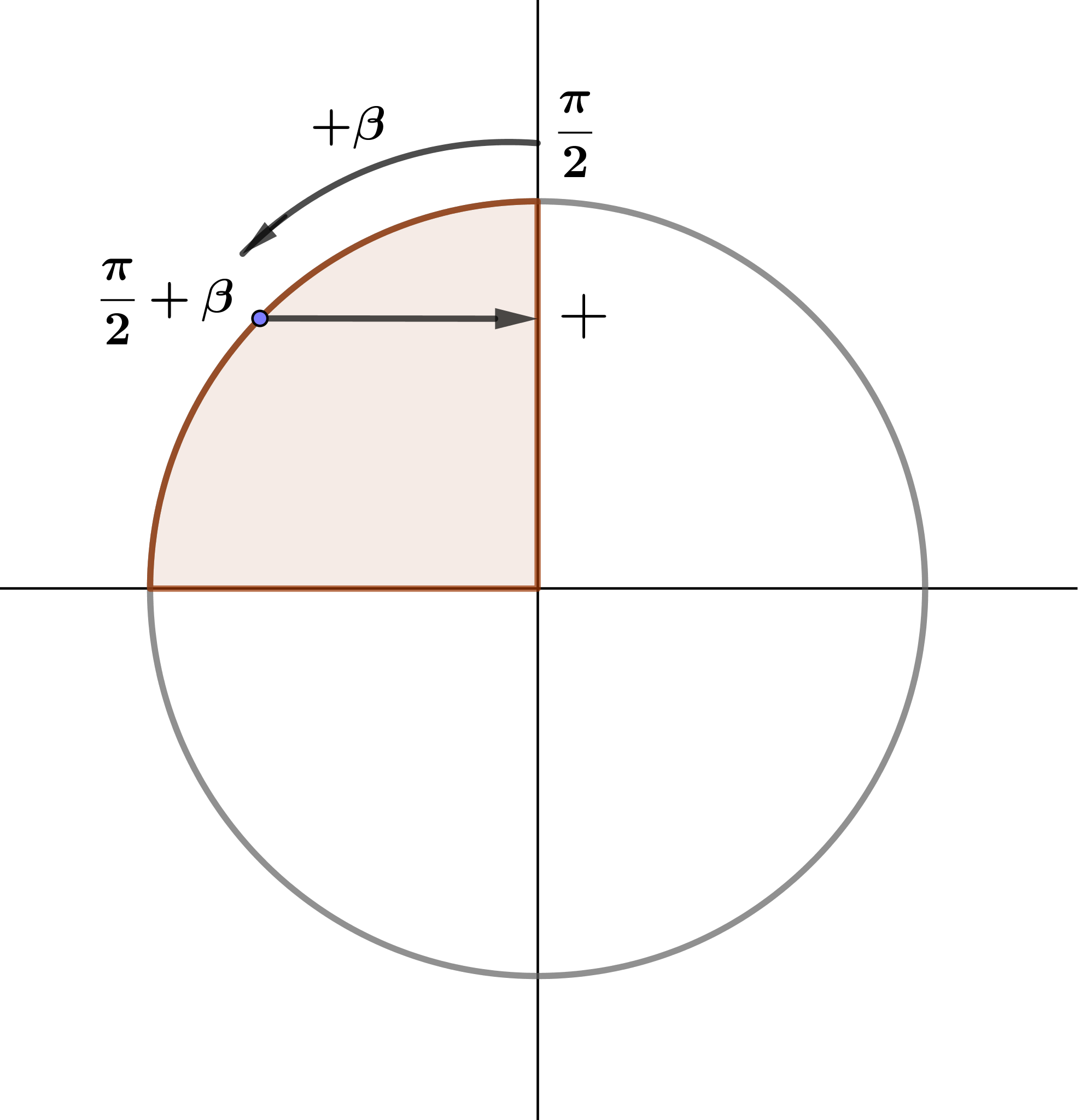
- \(\displaystyle \sin\left(\frac{\pi}{2} + \beta\right)=\cos\beta\)
- \(\displaystyle \cos(\beta + 3\pi)= \cos(3\pi+\beta)=-\cos\beta\)
Подставим полученные результаты в исходное выражение:
\(\displaystyle \frac{3\color{blue}{\cos(\pi - \beta)} + \color{green}{\sin\left(\dfrac{\pi}{2} + \beta\right)}} { \color{orange}{\cos(\beta + 3\pi)}}=\frac{3(\color{blue}{-\cos \beta} )+ \color{green}{\cos\beta}} { \color{orange}{-\cos\beta}}=\frac{-3\cos \beta + \cos\beta} { -\cos\beta}{\small .}\)
Упростим дробь:
\(\displaystyle \frac{-3\cos \beta + \cos\beta} { -\cos\beta}=\frac{-2\cos \beta} { -\cos\beta}=2{\small .}\)
Ответ: \(\displaystyle 2 {\small.} \)