Задание
Ребро куба равно \(\displaystyle 2\sqrt{3} {\small .}\) Найдите диагональ куба.
Решение
Проведем диагональ основания (квадрата), чтобы получить прямоугольный треугольник, гипотенуза которого является диагональ куба.
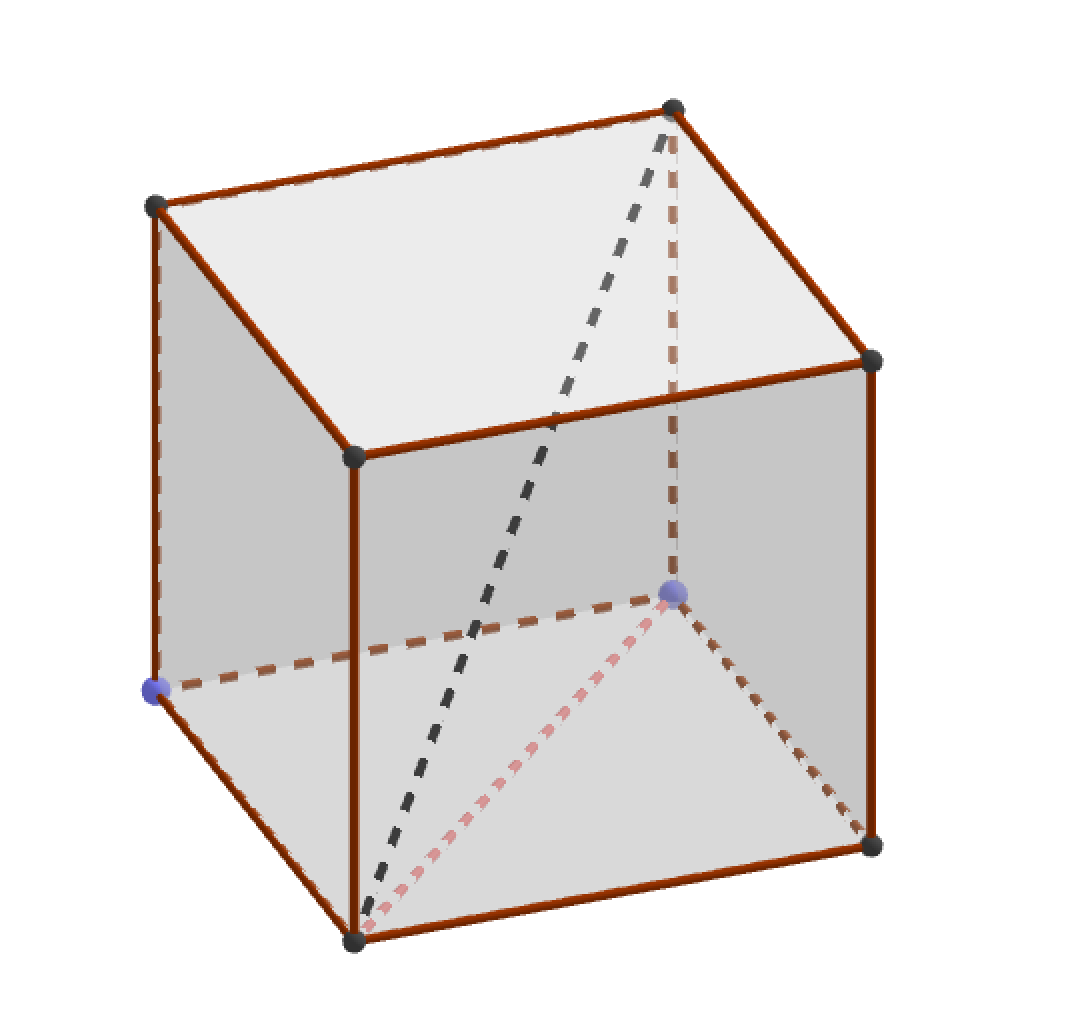
По теореме Пифагора найдем диагональ квадрата основания:
\(\displaystyle \sqrt{(2\sqrt{3})^2+(2\sqrt{3})^2}=\sqrt{24}=2\sqrt{6}.\)
Рассмотрим полученный прямоугольный треугольник:
 |  |
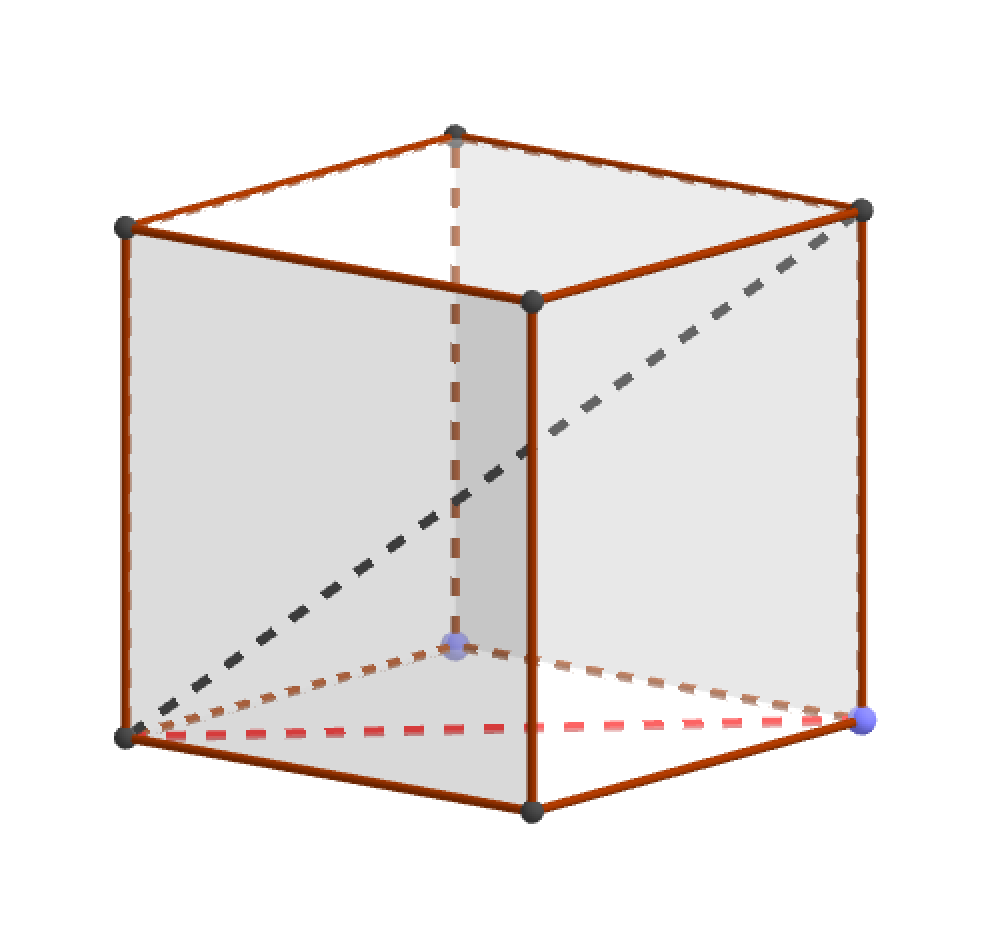Один катет – это ребро куба, второй катет – диагональ основания. Следовательно, гипотенуза данного прямоугольного треугольника равна
\(\displaystyle \sqrt{(2\sqrt{3})^2+(2\sqrt{6})^2}=\sqrt{12+24}=\sqrt{36}=6.\)
Ответ: \(\displaystyle 6{\small .}\)