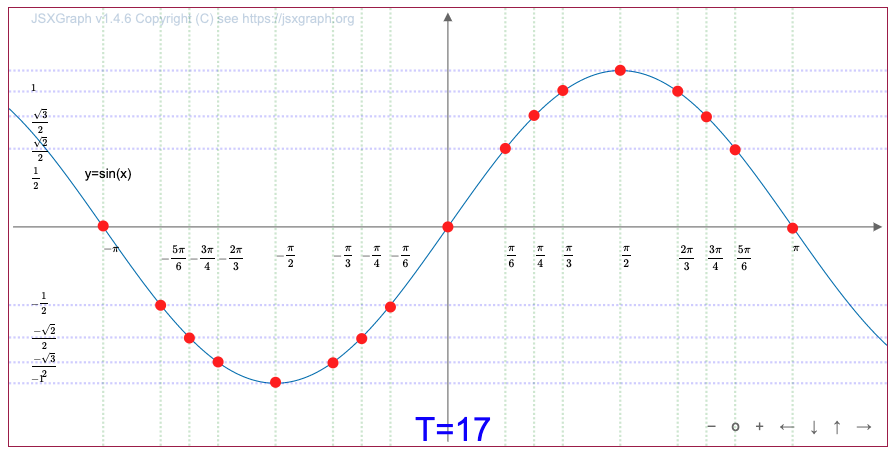
Расположите точки так, чтобы получился график функции \(\displaystyle y=\sin(x)\) на отрезке \(\displaystyle [-\pi;\, \pi]{\small .}\)
При каком значении T рисуется график?
\(\displaystyle T=17\)
\(\displaystyle \sin \left( \frac{\pi}{6} \right)=\frac{1}{2}{\small ,}\) \(\displaystyle \sin \left( \frac{\pi}{4} \right)=\frac{\sqrt{2}}{2}{\small ,}\)
\(\displaystyle \sin \left( \frac{\pi}{3} \right)=\frac{\sqrt{3}}{2}{\small ,}\) \(\displaystyle \sin \left( \frac{\pi}{2} \right)=1{\small ,}\)
- \(\displaystyle \sin \left( \frac{2\pi}{3} \right)=\sin \left(\pi- \frac{\pi}{3} \right)=\sin \left( \frac{\pi}{3} \right)=\frac{\sqrt{3}}{2}{\small ,}\)
- \(\displaystyle \sin \left( \frac{3\pi}{4} \right)=\sin \left(\pi- \frac{\pi}{4} \right)=\sin \left( \frac{\pi}{4} \right)=\frac{\sqrt{2}}{2}{\small ,}\)
- \(\displaystyle \sin \left( \frac{5\pi}{6} \right)=\sin \left(\pi- \frac{\pi}{6} \right)=\sin \left( \frac{\pi}{6} \right)=\frac{1}{2}{\small ,}\)
- \(\displaystyle \sin \left( \pi \right)=0{\small .}\)
Так как \(\displaystyle \sin(-x)=-\sin(x){\small ,}\) то
\(\displaystyle \sin \left( -\frac{\pi}{6} \right)=-\frac{1}{2}{\small ,}\) \(\displaystyle \sin \left( -\frac{\pi}{4} \right)=-\frac{\sqrt{2}}{2}{\small ,}\)
\(\displaystyle \sin \left(-\frac{\pi}{3} \right)=-\frac{\sqrt{3}}{2}{\small ,}\) \(\displaystyle \sin \left( -\frac{\pi}{2} \right)=-1{\small ,}\)
- \(\displaystyle \sin \left( -\frac{2\pi}{3} \right)=-\frac{\sqrt{3}}{2}{\small ,}\)
- \(\displaystyle \sin \left(- \frac{3\pi}{4} \right)=-\frac{\sqrt{2}}{2}{\small ,}\)
- \(\displaystyle \sin \left(- \frac{5\pi}{6} \right)=-\frac{1}{2}{\small ,}\)
- \(\displaystyle \sin \left( -\pi \right)=0{\small .}\)