Точка \(\displaystyle O\) – точка пересечения диагоналей \(\displaystyle AC\) и \(\displaystyle BD\) ромба \(\displaystyle ABCD \small.\) Найдите площадь ромба, если площадь треугольника \(\displaystyle ABO \) равна \(\displaystyle 10 \small.\)

По свойству ромба диагонали \(\displaystyle AC\) и \(\displaystyle BD\) перпендикулярны, по свойству параллелограмма они делятся пополам точкой \(\displaystyle O \small.\) Тогда прямоугольные треугольники \(\displaystyle AOB \small,\) \(\displaystyle COB \small,\) \(\displaystyle COD\) и \(\displaystyle AOD\) равны по двум катетам.
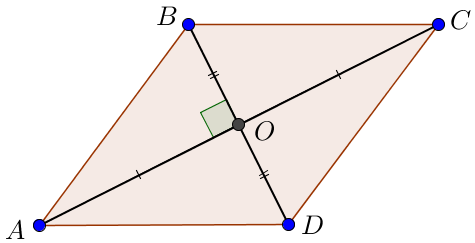
Значит, у треугольников \(\displaystyle AOB \small,\) \(\displaystyle BOC \small,\) \(\displaystyle COD\) и \(\displaystyle DOA\) равные площади и
\(\displaystyle S_{ABCD}={4} \cdot S_{ABO}=4 \cdot 10= 40 \small.\)
Ответ: \(\displaystyle 40 {\small .}\)