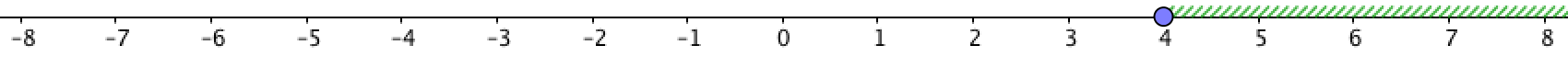СВОДНАЯ ТАБЛИЦА ЧИСЛОВЫХ ПРОМЕЖУТКОВ
| Аналитическая модель | Геометрическая модель | Обозначение | Название |
| \(\displaystyle x>a\) | 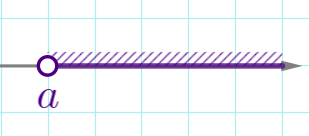 | \(\displaystyle (a;+ \infty)\) | открытый луч |
| \(\displaystyle x \geq a\) | 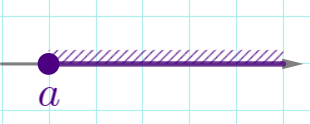 | \(\displaystyle [a;+ \infty)\) | замкнутый луч |
| \(\displaystyle x<b\) | 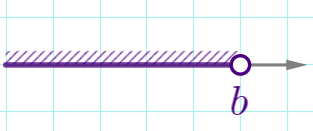 | \(\displaystyle (- \infty;b)\) | открытый луч |
| \(\displaystyle x \leq b\) | 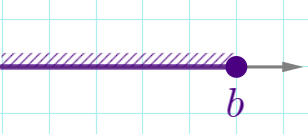 | \(\displaystyle (- \infty;b]\) | замкнутый луч |
| \(\displaystyle a<x<b\) | 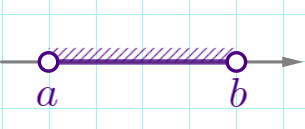 | \(\displaystyle (a;b)\) | интервал |
| \(\displaystyle a \leq x \leq b\) | 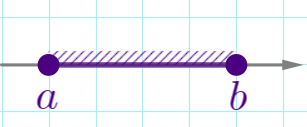 | \(\displaystyle [a;b]\) | отрезок |
| \(\displaystyle a \leq x < b\) | 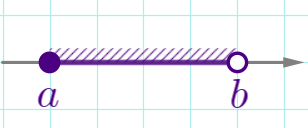 | \(\displaystyle [a;b)\) | полуинтервал |
| \(\displaystyle a < x \leq b\) | 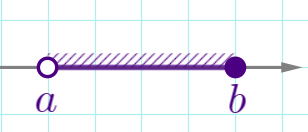 | \(\displaystyle (a;b]\) | полуинтервал |
\(\displaystyle \color{blue}{(-\infty;\,-4)}\)
По определению, \(\displaystyle (-\infty; \,-4)\) – это множество всех чисел, координаты которых меньше \(\displaystyle -4{\small .}\)
Точки, соответствующие данному интервалу, изображаются так:
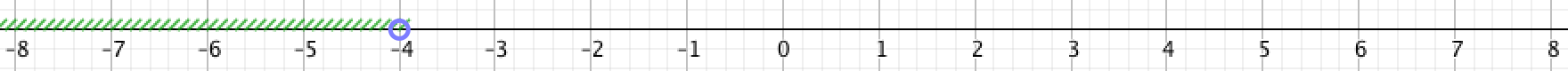
\(\displaystyle \color{blue}{(-\infty;\,-4]}\)
По определению, \(\displaystyle (-\infty; \,-4]\) – это множество всех чисел, координаты которых меньше \(\displaystyle -4{\small ,}\) включая точку с координатой \(\displaystyle -4{\small .}\)
Точки, соответствующие данному полуинтервалу, изображаются так:

\(\displaystyle \color{blue}{(2;+\infty)}\)
По определению, \(\displaystyle (2;+\infty)\) – это множество всех чисел, координаты которых больше \(\displaystyle 2{\small .}\)
Точки, соответствующие данному интервалу, изображаются так:

\(\displaystyle \color{blue}{[4;+\infty)}\)
По определению, \(\displaystyle [4;+\infty)\) – это множество всех чисел, координаты которых больше \(\displaystyle 4{\small ,}\) включая точку с координатой \(\displaystyle 4{\small .}\)
Точки, соответствующие данному полуинтервалу, изображаются так: