Диагонали параллелограмма \(\displaystyle MNKP\) пересекаются в точке \(\displaystyle O{\small.}\) Найдите периметр треугольника \(\displaystyle ONK{\small,}\) если \(\displaystyle MK=18\, {\footnotesize см}{\small,}\) \(\displaystyle OP=5\, {\footnotesize см}{\small,}\) \(\displaystyle MP=11\, {\footnotesize см}{\small.}\)
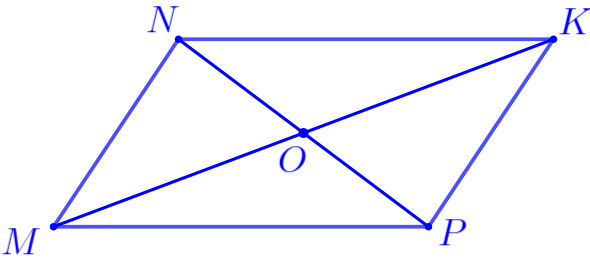
\(\displaystyle P_{\triangle ONK}=\) см
\(\displaystyle MNKP\) – параллелограмм:
| 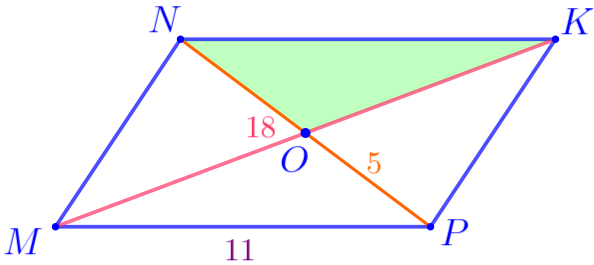 |
Требуется найти периметр треугольника \(\displaystyle ONK{\small:}\)
\(\displaystyle P_{\triangle ONK}=ON+OK+NK={\Large \color{red}?}\)
Найдем длины отрезков \(\displaystyle ON{\small,}\) \(\displaystyle OK\) и \(\displaystyle NK{\small.}\)
Свойство параллелограмма
 | Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам. |
В параллелограмме \(\displaystyle MNKP\) получаем:
\(\displaystyle ON=OP=5\, {\footnotesize см}{\small,}\)
\(\displaystyle OK=OM=\frac{MK}{2}=\frac{18}{2}=9\, {\footnotesize см}{\small.}\) | 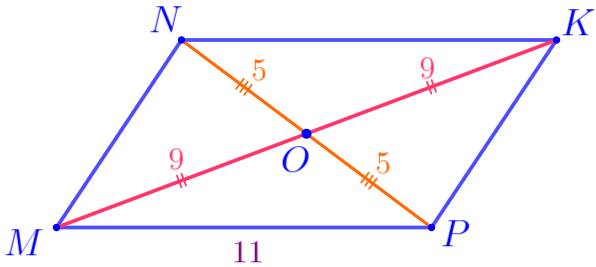 |
Свойство параллелограмма
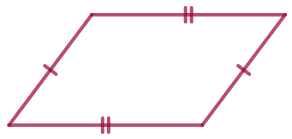 | Противоположные стороны параллелограмма попарно равны. |
В параллелограмме \(\displaystyle MNKP\) получаем:
\(\displaystyle NK=MP=11\, {\footnotesize см}{\small.}\) | 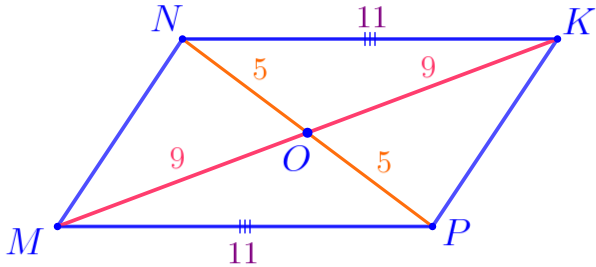 |
Подставим \(\displaystyle ON=5{\small,}\) \(\displaystyle OK=9{\small,}\) \(\displaystyle NK=11\) в формулу периметра:
\(\displaystyle P_{\triangle ONK}=ON+OK+NK=5+9+11=25\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle 25\, {\footnotesize см}{\small.}\)