Найдите площадь ромба, сторона которого равна \(\displaystyle 9{\small,}\) а высота равна \(\displaystyle 7{\small.}\)
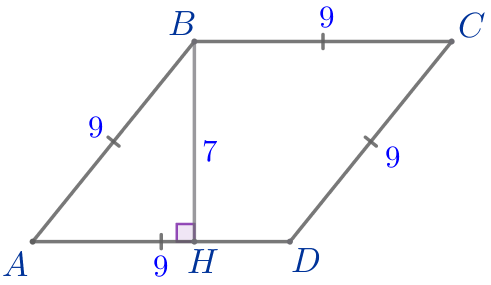 | Пусть \(\displaystyle ABCD\) – ромб:
\(\displaystyle AB=BC=CD=AD=9{\small;}\)
Требуется найти площадь данного ромба. |
Воспользуемся одной из формул для вычисления площади ромба.
Формула площади ромба
\(\displaystyle S=h\cdot a \small,\)
где \(\displaystyle h\) – высота ромба,
\(\displaystyle a \) – сторона ромба.
В данном случае площадь ромба равна произведению высоты \(\displaystyle BH\) на сторону \(\displaystyle AD{\small : } \)
\(\displaystyle {S_{ромб}} = {BH }\cdot AD {\small.}\)
Тогда
\(\displaystyle {S_{ромб}} =7 \cdot 9= 63 {\small.}\)
Ответ: \(\displaystyle 63{\small .}\)