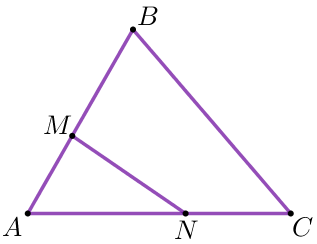
На сторонах \(\displaystyle AB\) и \(\displaystyle AC\) треугольника \(\displaystyle ABC\) отмечены точки \(\displaystyle M\) и \(\displaystyle N\) соответственно. Известно, что \(\displaystyle AM:AB=3:7\) и \(\displaystyle AN:AC=3:5 {\small.}\) Найдите площадь треугольника \(\displaystyle AMN {\small,}\) если площадь треугольника \(\displaystyle ABC\) равна \(\displaystyle 70 {\small.}\)
Теорема о площадях треугольников с равными углами
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы: \(\displaystyle \frac{\color{blue}{S_{\triangle ABC}}}{\color{green}{S_{\triangle MNK}}}=\frac{\color{blue}{AB} \cdot \color{blue}{AC}}{\color{green}{MN} \cdot \color{green}{MK}} \) | 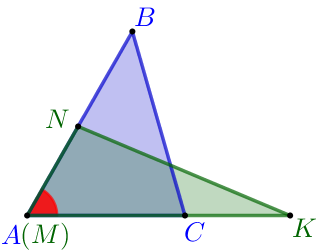 |
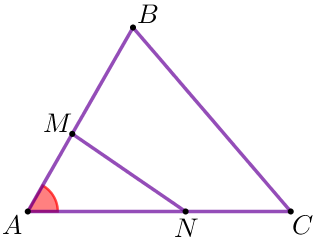 | В треугольниках \(\displaystyle AMN\) и \(\displaystyle ABC\) \(\displaystyle \angle MAN= \angle BAC {\small.}\) По теореме о площадях треугольников с равными углами получаем: \(\displaystyle \frac{S_{\triangle AMN}}{S_{\triangle ABC}}=\frac{AM \cdot AN}{AB \cdot AC} \ {\small.}\) |
По условию \(\displaystyle \frac{AM}{AB}=\frac{3}{7} \) и \(\displaystyle \frac{AN}{AC}=\frac{3}{5} {\small,}\) тогда
\(\displaystyle \frac{S_{\triangle AMN}}{S_{\triangle ABC}}=\frac{3}{7} \cdot \frac{3}{5} \ {\small,} \\ \)
\(\displaystyle \frac{S_{\triangle AMN}}{S_{\triangle ABC}}=\frac{9}{35} \ {\small.}\)
Из последнего равенства по пропорции получаем
\(\displaystyle S_{\triangle AMN}=\frac{9 \cdot S_{\triangle ABC}}{35} \ {\small,}\)
\(\displaystyle S_{\triangle AMN}=\frac{9 \cdot 70}{35}=9 \cdot 2=18{\small.}\)
Ответ: \(\displaystyle 18 {\small.}\)