В равнобедренной трапеции с перпендикулярными диагоналями высота равна \(\displaystyle 17{\small.}\) Найдите длину средней линии этой трапеции.
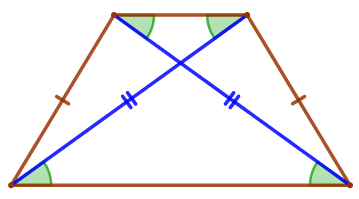
Пусть \(\displaystyle ABCD\) – равнобедренная трапеция:
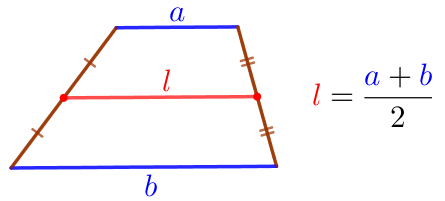
Требуется найти длину \(\displaystyle \color{red}{l}\) средней линии этой трапеции. | 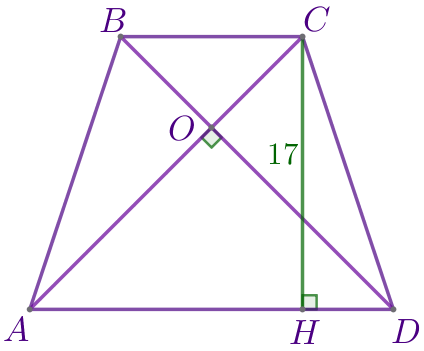 |
\(\displaystyle \color{red}{l}=\frac{BC+AD}{2}=\color{red}{\Large ?}\)
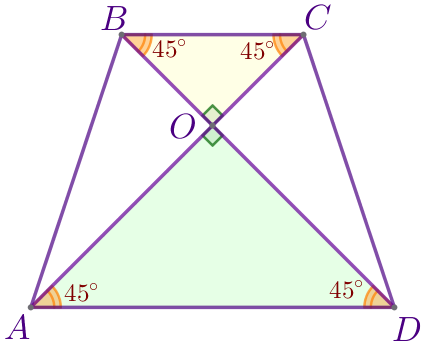
\(\displaystyle \angle OBC=\angle OCB=\angle OAD=\angle ODA=45^{\circ}{\small.}\)
Через точку пересечения диагоналей проведём высоту \(\displaystyle PF{\small.}\)
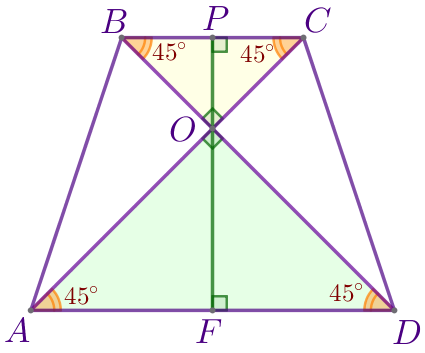 |
|
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы. Значит, \(\displaystyle OP=\frac{1}{2}\cdot BC{\small;}\) \(\displaystyle OF=\frac{1}{2}\cdot AD{\small.}\) | |
Так как точка \(\displaystyle O\) лежит на отрезке \(\displaystyle PF{\small,}\) то
\(\displaystyle PF=OP+OF{\small;}\\ \)
\(\displaystyle PF=\frac{1}{2}\cdot BC+\frac{1}{2}\cdot AD{\small;}\\ \)
\(\displaystyle PF=\frac{BC+AD}{2}{\small.}\)
В результате получили, что длина средней линии равнобедренной трапеции, у которой диагонали перпендикулярны, равна высоте этой трапеции. То есть
\(\displaystyle \color{red}{l}=PF{\small.}\)
Так как высоты трапеции равны, то \(\displaystyle PF=17{\small.}\) Значит, длина средней линии этой трапеции равна \(\displaystyle 17{\small.}\)
Ответ: \(\displaystyle 17{\small.}\)