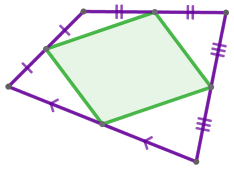
Точки \(\displaystyle K{\small,}\) \(\displaystyle L{\small,}\) \(\displaystyle M{\small,}\) \(\displaystyle N\) – середины сторон \(\displaystyle AB{\small,}\) \(\displaystyle BC{\small,}\) \(\displaystyle CD\) и \(\displaystyle DE\) выпуклого пятиугольника \(\displaystyle ABCDE\) соответственно. Точки \(\displaystyle F\) и \(\displaystyle T\) – середины отрезков \(\displaystyle KM\) и \(\displaystyle LN\) соответственно. Найдите длину отрезка \(\displaystyle FT{\small,}\) если \(\displaystyle AE=12{\small.}\)
\(\displaystyle FT=\)
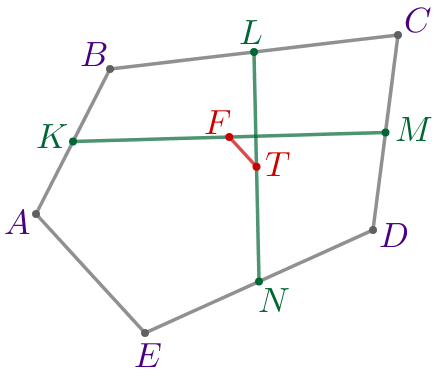
 | \(\displaystyle ABCDE\) – выпуклый пятиугольник:
|
Требуется найти длину отрезка \(\displaystyle FT{\small.}\)
Выполним дополнительное построение. Соединим отрезком точки \(\displaystyle A\) и \(\displaystyle D{\small.}\) Пусть точка \(\displaystyle P\) – середина отрезка \(\displaystyle AD{\small.}\)
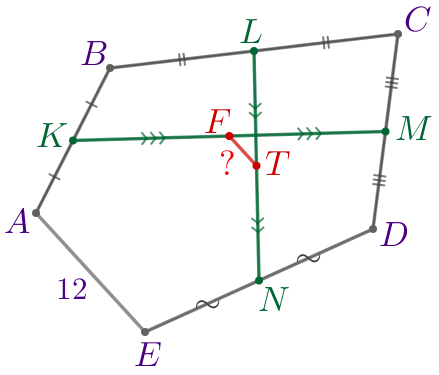
В четырёхугольнике \(\displaystyle ABCD\) точки \(\displaystyle K{\small,}\) \(\displaystyle L{\small,}\) \(\displaystyle M\) и \(\displaystyle P\) являются серединами сторон \(\displaystyle AB{\small,}\) \(\displaystyle BC{\small,}\) \(\displaystyle CD\) и \(\displaystyle AD\) соответственно. | 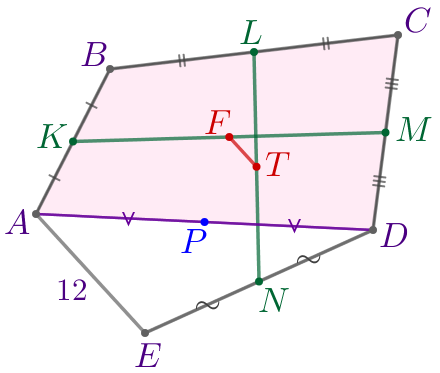 |
\(\displaystyle KLMP\) – параллелограмм.
Диагонали параллелограмма точкой пересечения делятся пополам.
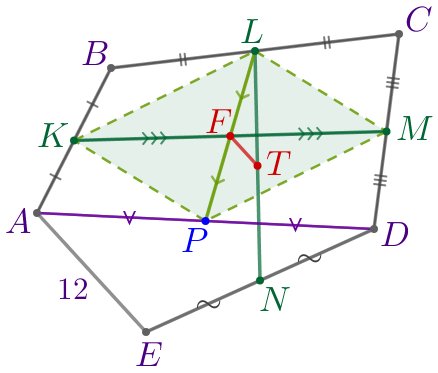 | \(\displaystyle LP\) и \(\displaystyle KM\) – диагонали параллелограмма \(\displaystyle KLMP{\small.}\) Точка \(\displaystyle F\) – середина диагонали \(\displaystyle KM{\small,}\) значит, \(\displaystyle F\) – точка пересечения диагоналей. Следовательно, точка \(\displaystyle F\) делит диагональ \(\displaystyle LP\) пополам. То есть \(\displaystyle LF=FP{\small.}\) |
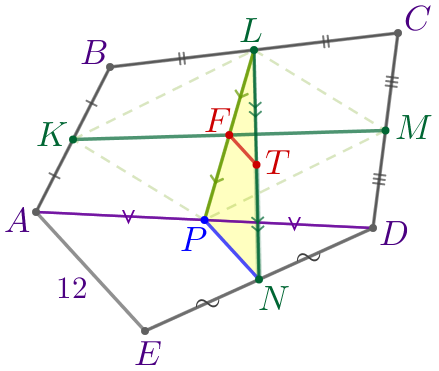 |
Cледовательно, \(\displaystyle FT\) – средняя линия треугольника \(\displaystyle LNP{\small.}\) Значит, \(\displaystyle FT \parallel PN\) и \(\displaystyle FT=\frac{1}{2}\cdot PN{\small.}\) |
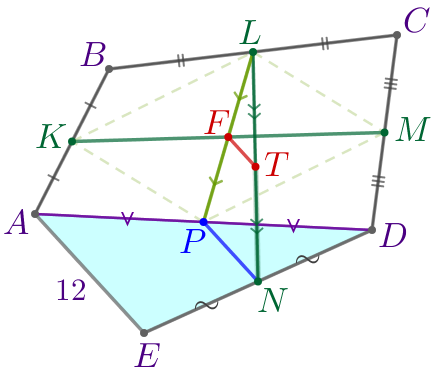 |
Cледовательно, \(\displaystyle PN\) – средняя линия треугольника \(\displaystyle ADE{\small.}\) Значит, \(\displaystyle PN \parallel AE\) и \(\displaystyle PN=\frac{1}{2}\cdot AE{\small.}\) Подставим \(\displaystyle AE=12{\small:}\) \(\displaystyle PN=\frac{1}{2}\cdot 12=6{\small.}\) |
Тогда
\(\displaystyle FT=\frac{1}{2}\cdot PN=\frac{1}{2}\cdot 6=3{\small.}\)
Ответ: \(\displaystyle FT=3{\small.}\)