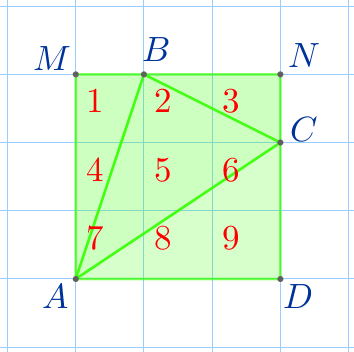
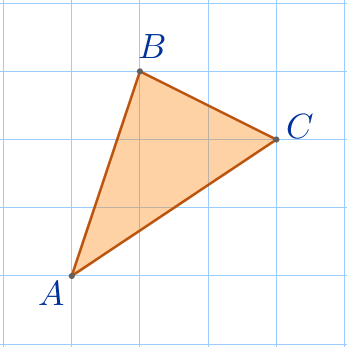
На рисунке изображен треугольник \(\displaystyle ABC\) с вершинами в узлах квадратной сетки. Найдите площадь данного треугольника, если известно, что площадь клетки равна \(\displaystyle 4\, {\footnotesize см^{2}}{\small.}\)
\(\displaystyle S_{\triangle ABC}=\)\(\displaystyle {\footnotesize см^{2}}{\small.}\)
\(\displaystyle \color{blue}{1)}\) Найдём площадь треугольника \(\displaystyle ABC\) в клетках.
Выполним дополнительное построение.
Через вершины треугольника \(\displaystyle ABC\) по линиям сетки вокруг данного треугольника опишем квадрат \(\displaystyle AMND{\small.}\)
| 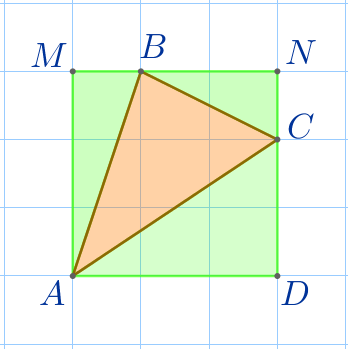 |
\(\displaystyle S_{AMND}=S_{\triangle ABC}+S_{\triangle AMB}+S_{\triangle BNC}+S_{\triangle ACD}{\small.}\)
Выразим площадь треугольника \(\displaystyle ABC{\small:}\)
\(\displaystyle S_{\triangle ABC}=S_{AMND}-(S_{\triangle AMB}+S_{\triangle BNC}+S_{\triangle ACD}){\small.}\)
По рисунку найдём площади (в клетках) квадрата и треугольников из правой части равенства.
\(\displaystyle S_{AMND}=9{\small.}\)
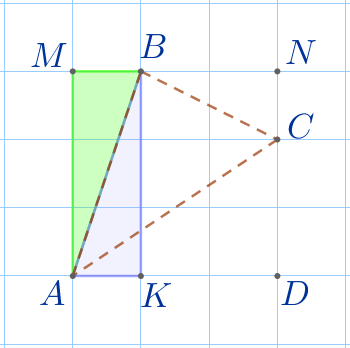
\(\displaystyle S_{\triangle AMB}=1{,}5{\small.}\)
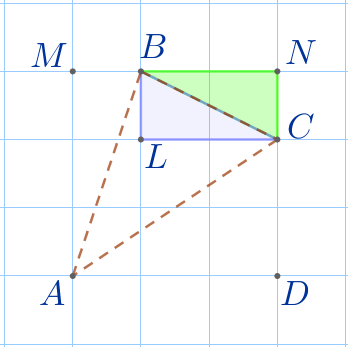
\(\displaystyle S_{\triangle BNC}=1{\small.}\)
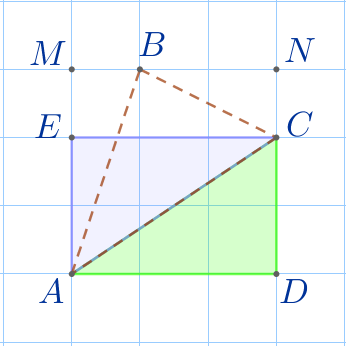
\(\displaystyle S_{\triangle ACD}=3{\small.}\)
В результате получаем:
\(\displaystyle S_{\triangle ABC}=9-(1{,}5+1+3)=9-5{,}5=3{,}5{\small.}\)
\(\displaystyle \color{blue}{2)}\) Вычислим площадь треугольника \(\displaystyle ABC\) в квадратных сантиметрах.
Так как площадь одной клетки равна \(\displaystyle 4\, {\footnotesize см^{2}}{\small,}\) а площадь треугольника \(\displaystyle ABC\) составляет \(\displaystyle 3{,}5\) клетки, то
\(\displaystyle S_{\triangle ABC}=4\, ({\footnotesize см^{2}})×3{,}5\, ({\footnotesize клетки})=14\,({\footnotesize см^{2}}){\small.}\)
Ответ: \(\displaystyle S_{\triangle ABC}=14\,{\footnotesize см^{2}}{\small.}\)