Выберите тригонометрическое выражение, равное данному:
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\)
Каждое из выражений
\(\displaystyle \sin\left(\frac{\pi}{2}\pm \alpha\right),\, \cos\left(\frac{\pi}{2}\pm \alpha\right),\, \sin\left(\frac{3\pi}{2}\pm \alpha\right),\, \cos\left(\frac{3\pi}{2}\pm \alpha\right),\, \sin\left(\alpha-\frac{\pi}{2}\right),\, \cos\left(\alpha-\frac{\pi}{2}\right),\)
\(\displaystyle \sin\left(\pi\pm \alpha\right),\, \cos\left(\pi\pm \alpha\right), \, \sin\left(\alpha-\pi \right),\, \cos\left(\alpha-\pi\right)\)
равно либо \(\displaystyle \pm\sin\alpha{ \small ,}\) либо \(\displaystyle \pm\cos\alpha{\small .}\)
- Если в формуле участвует \(\displaystyle \frac{\pi}{2} \) или \(\displaystyle \frac{3\pi}{2} { \small ,}\) то синус меняется на косинус, а косинус меняется на синус, иначе функция не меняется.
- Знак синуса и косинуса определяется по знаку исходного выражения, при условии, что угол \(\displaystyle 0<\alpha<\frac{\pi}{2}{\small .}\)
Так как в выражении \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)\) участвует \(\displaystyle \frac{\pi}{2}{ \small ,}\) то
\(\displaystyle {\bf \cos}\left(\frac{\pi}{2}-\alpha\right)=\,?\,{\bf \sin}\alpha{\small .}\)
Далее определим, какой знак должен стоять перед синусом.
Всегда можно считать, что угол \(\displaystyle \alpha\) – острый (располагается в первой четверти тригонометрического круга):
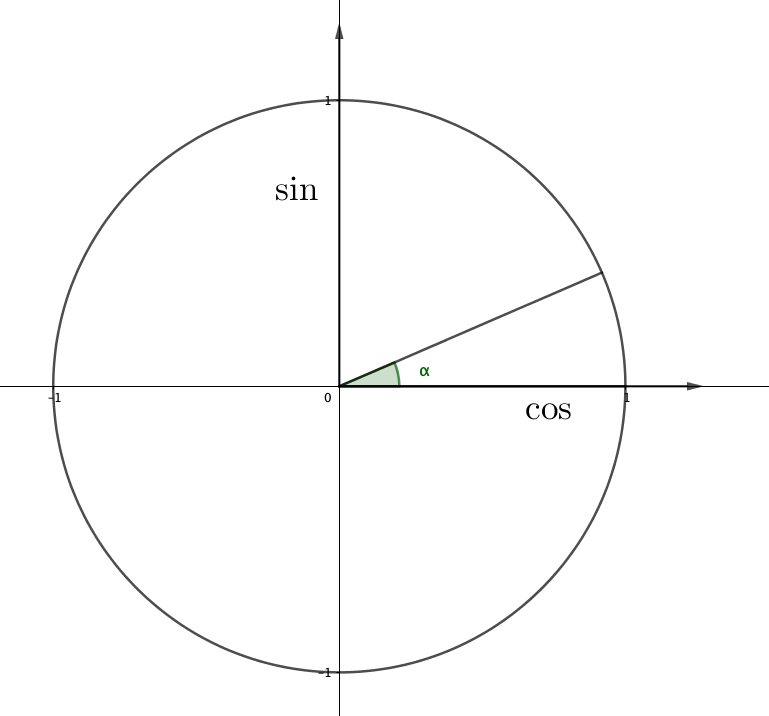
Тогда угол \(\displaystyle \frac{\pi}{2}-\alpha\) – это угол, полученный вычитанием угла \(\displaystyle \alpha \) из угла \(\displaystyle \frac{\pi}{2}{\small :}\)

Определим знак исходного выражения, то есть знак \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right){\small : }\)
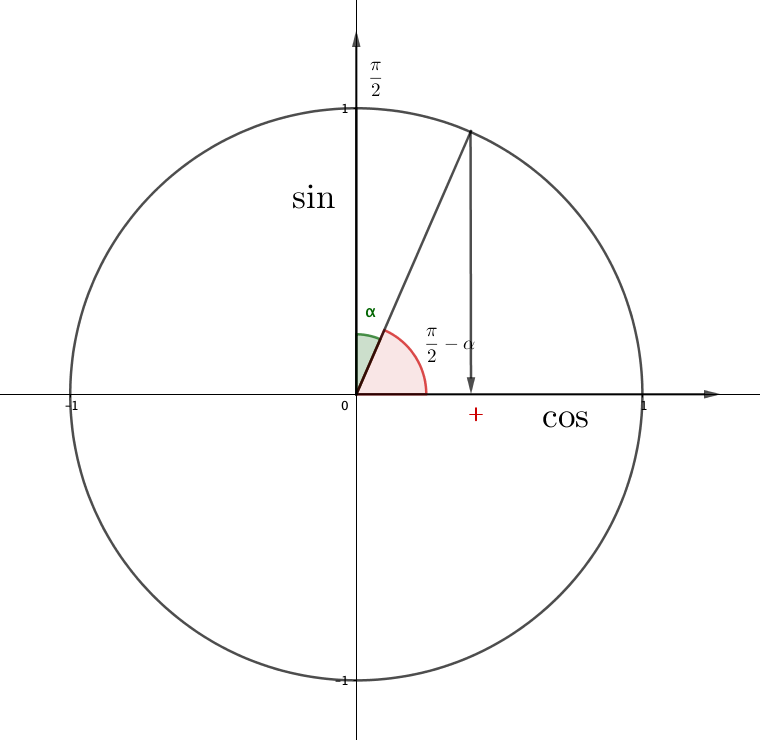
Знак плюс. Значит,
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\color{red}{+}\sin{\alpha}\)
или
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin{\alpha}{\small .}\)
Ответ: \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin{\alpha}{\small .}\)
Используем формулу косинуса разности.
Для двух углов \(\displaystyle x\) и \(\displaystyle y\) верно:
\(\displaystyle \cos(x-y)=\cos x\cdot \cos y+\sin x\cdot \sin y{\small .}\)
Тогда
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\cos\frac{\pi}{2}\cdot \cos\alpha+\sin\frac{\pi}{2}\cdot \sin\alpha{\small .}\)
Так как \(\displaystyle \cos\frac{\pi}{2}=0\) и \(\displaystyle \sin\frac{\pi}{2}=1{ \small ,}\) то получаем:
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=0\cdot \cos\alpha+1\cdot \sin\alpha{ \small ,}\)
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha{\small .}\)
Ответ: \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha{\small .}\)