В равнобедренную трапецию, периметр которой равен \(\displaystyle 100{\small,}\) а площадь равна \(\displaystyle 500 {\small,}\) можно вписать окружность. Найдите длины оснований трапеции.
Меньшее основание трапеции равно \(\displaystyle ;\)
бóльшее основание трапеции равно \(\displaystyle .\)
По условию задачи построим чертёж.
Пусть \(\displaystyle ABCD\) – равнобедренная трапеция, в которую вписана окружность, при этом:
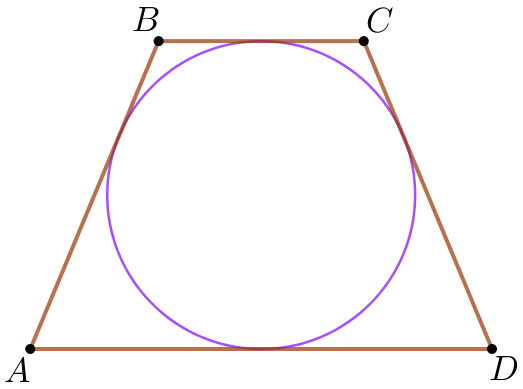 |
По условию:
|
Требуется найти длины оснований трапеции.
Сначала найдем боковую сторону и высоту трапеции.
По условию задачи в равнобедренную трапецию вписана окружность.
\(\displaystyle AD+BC=AB+CD {\small.}\)
Периметр трапеции – это сумма длин всех сторон трапеции.
\(\displaystyle P_{ABCD}=AD+BC+AB+CD {\small.}\)
Следовательно, сумма оснований и сумма боковых сторон равна половине периметра:
\(\displaystyle AD+BC=AB+CD=\frac{1}{2} \cdot P_{ABCD}=\frac{1}{2}\cdot 100=50{\small.}\)
Так как трапеция равнобедренная \(\displaystyle (AB=CD) {\small,}\) то
\(\displaystyle AB+CD =2 \cdot AB {\small.}\)
Получаем
\(\displaystyle AD+BC=2\cdot AB=50{\small;}\\ \)
\(\displaystyle \frac{AD+BC}{2}=AB=25{\small.} \)
Далее найдём высоту трапеции.
Из точки \(\displaystyle B\) построим перпендикуляр \(\displaystyle BH\) к основанию\(\displaystyle AD{\small.}\) \(\displaystyle BH\)– высота трапеции \(\displaystyle ABCD{\small.}\)
| 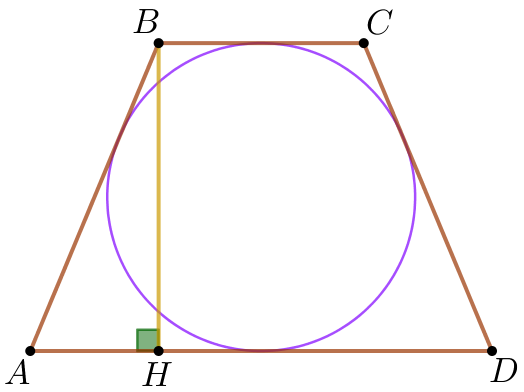 |
Воспользуемся формулой площади трапеции.
Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
| \(\displaystyle S=\frac{\color{blue}{a}+\color{blue}{b}}{2}\cdot \color{red}{h}\) |
Получаем
\(\displaystyle S_{ABCD}= \frac{AD+BC}{2} \cdot BH{\small.}\\ \)
Подставим в формулу площади известные значения \(\displaystyle (S_{ABCD}=500{\small,} \) \(\displaystyle \frac{AD+BC}{2}=25) \) и найдем \(\displaystyle BH{\small:}\\ \)
\(\displaystyle 500=25 \cdot BH{\small,}\)
\(\displaystyle BH=20{\small.}\)
Найдем основания \(\displaystyle BC\) и \(\displaystyle AD{\small.}\)
Выполним дополнительное построение.
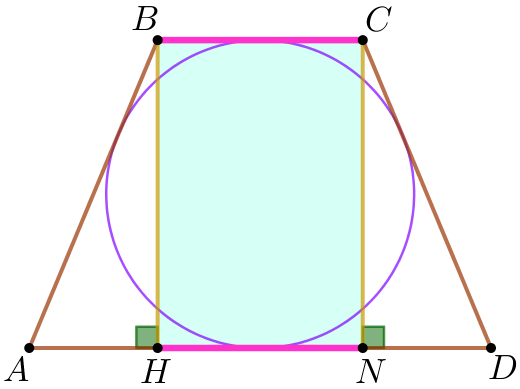 | Из вершины \(\displaystyle C\) опустим перпендикуляр \(\displaystyle CN\) на основание на \(\displaystyle AD {\small.}\) \(\displaystyle BH=CN=20\) – высоты трапеции. \(\displaystyle BCNH\) – прямоугольник. Значит, \(\displaystyle HN=BC {\small.}\) Тогда \(\displaystyle AD=AH+BC+DN {\small.}\) |
Рассмотрим прямоугольные треугольники \(\displaystyle ABH\) и \(\displaystyle DCN {\small.}\)
Значит,\(\displaystyle \triangle ABH= \triangle DCN\) (по гипотенузе и катету). Следовательно, \(\displaystyle AH=DN {\small.}\) | 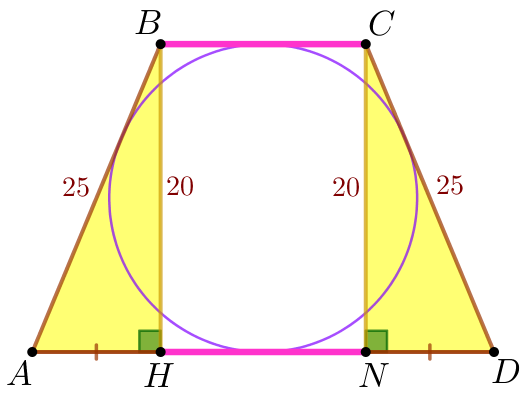 |
Из треугольника \(\displaystyle ABH\) по теореме Пифагора
\(\displaystyle AH^2=AB^2-BH^2 {\small;}\)
\(\displaystyle AH^2=25^2-20^2=625-400=225=15^2 {\small.}\)
Так как длина отрезка не может быть отрицательной, то \(\displaystyle AH=15 {\small.}\)
Получаем
\(\displaystyle AD=AH+BC+DN {\small;}\)
\(\displaystyle AD=15+BC+15=BC+30{\small.}\)
Зная сумму оснований, найдем длины оснований \(\displaystyle BC\) и \(\displaystyle AD{\small.}\)
\(\displaystyle AD+BC=50 {\small;}\)
\(\displaystyle BC+30+BC=50 {\small;}\)
\(\displaystyle 2 \cdot BC=20 {\small;}\)
\(\displaystyle BC=10{\small;}\)
\(\displaystyle AD=50-BC=50-10=40{\small.}\)
Ответ: \(\displaystyle BC=10{\small;}\) \(\displaystyle AD=40{\small.}\)