Основания равнобедренной трапеции равны \(\displaystyle 21\) и \(\displaystyle 5\small,\) высота равна \(\displaystyle 8\small.\) Найдите острый угол трапеции. Ответ дайте в градусах.
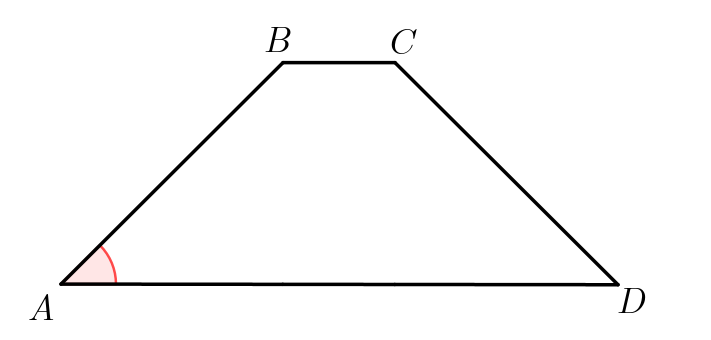
Пусть \(\displaystyle AD=21\) и \(\displaystyle BC=5\) – основания, \(\displaystyle AB=CD\) – боковые стороны, \(\displaystyle BH=CK=8 \) – высоты равнобедренной трапеции \(\displaystyle ABCD\small.\) Поскольку основания трапеции параллельны, а высоты трапеции перпендикулярны основаниям, \(\displaystyle BH K C \) – прямоугольник. Тогда \(\displaystyle H K =BC=5 \small.\) | 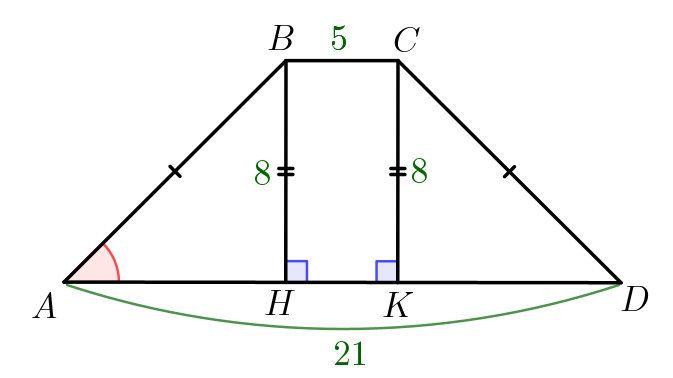 |
Прямоугольные треугольники \(\displaystyle ABH\) и \(\displaystyle DCK\) равны по гипотенузе \(\displaystyle AB=CD\) и катету \(\displaystyle BH=CK\small.\) Значит, \(\displaystyle AH=DK\) и \(\displaystyle AH=DK=\frac{AD-BC}{2}\small,\) \(\displaystyle AH=\frac{21-5}{2}=\frac{16}{2}=8\small.\) | 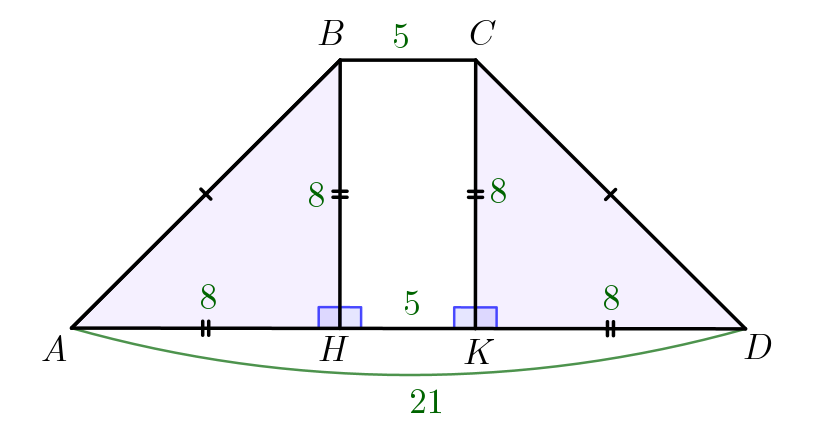 |
Острый угол трапеции найдем из треугольника \(\displaystyle CKD\small.\) Так как \(\displaystyle CK=KD=8\small,\) то треугольник \(\displaystyle CKD\) – равнобедренный. Тогда, по свойству равнобедренного треугольника, \(\displaystyle \angle KCD=\angle KDC\small.\) Сумма углов треугольника равна \(\displaystyle 180^{\circ}\small,\) поэтому \(\displaystyle \angle KCD=\frac{1}{2}(180^{\circ}-\angle CKD )\small,\) \(\displaystyle \angle KCD=\frac{1}{2}(180^{\circ}-90^{\circ})=\frac{1}{2}\cdot 90^{\circ}=45^{\circ}\small.\) | 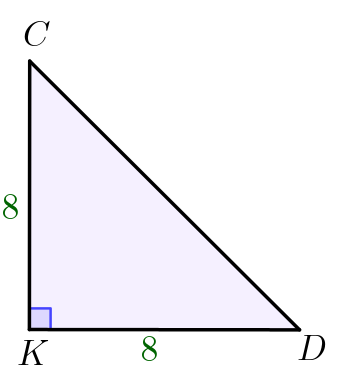 |
Ответ: \(\displaystyle 45 \small.\)