В равнобедренной трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AD\) и \(\displaystyle BC\) \(\displaystyle O\) – точка пересечения диагоналей, \(\displaystyle BD=12\sqrt{2}\small,\) \(\displaystyle OC=5\sqrt{2}\small,\) \(\displaystyle \angle AOD=90^\circ\small.\) Найдите \(\displaystyle AD\small.\)
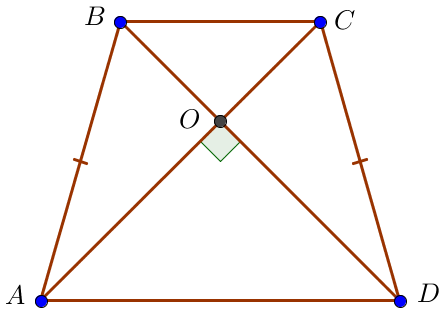
Рассмотрим треугольники \(\displaystyle ABD\) и \(\displaystyle ACD\small.\) Они равны по двум сторонам и углу между ними:
Значит, \(\displaystyle AC=BD=12\sqrt{2}\) и \(\displaystyle \angle ADB=\angle DAC\small.\) | 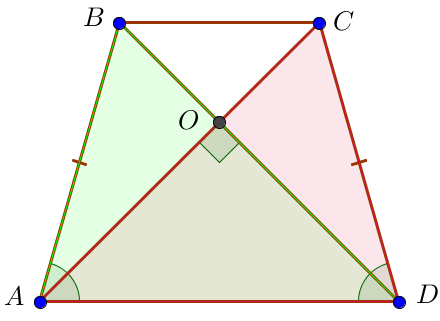 |
Тогда
\(\displaystyle AO=AC-OC=12\sqrt{2}-5\sqrt{2}=7\sqrt{2}\small.\)
Рассмотрим прямоугольный треугольник \(\displaystyle AOD\small.\) \(\displaystyle \angle OAD = \angle ODA\small,\) то треугольник \(\displaystyle AOD\) равнобедренный, \(\displaystyle AO=OD=7\sqrt{2}\small. \) По теореме Пифагора \(\displaystyle AD^2=AO^2 + OD^2=(7\sqrt{2})^2+(7\sqrt{2})^2=\) \(\displaystyle =98+98=196=14^2\small.\) | 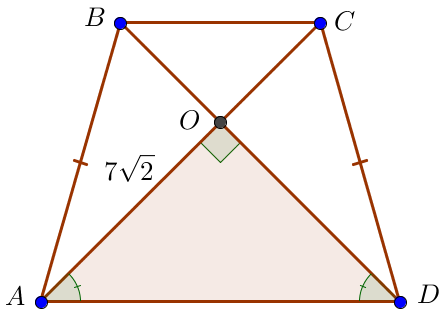 |
Поскольку длина отрезка положительна, то \(\displaystyle AD=14\small.\)
Ответ: \(\displaystyle 14{\small .}\)