Skip to main content

Теория: Движение по и против течения (короткая версия)

Задание

Скорость моторной лодки в стоячей воде \(\displaystyle 31{,}6\) км/ч. Скорость течения реки \(\displaystyle 4{,}2\) км/ч. Найдите скорость лодки при движении по течению реки и против течения реки.

\(\displaystyle v_{при\, \,движении\, \,против\, \,течения}=\)
27,4
  км/ч
\(\displaystyle v_{при\, \,движении\, \,по\, \,течению}=\)
35,8
  км/ч
Решение

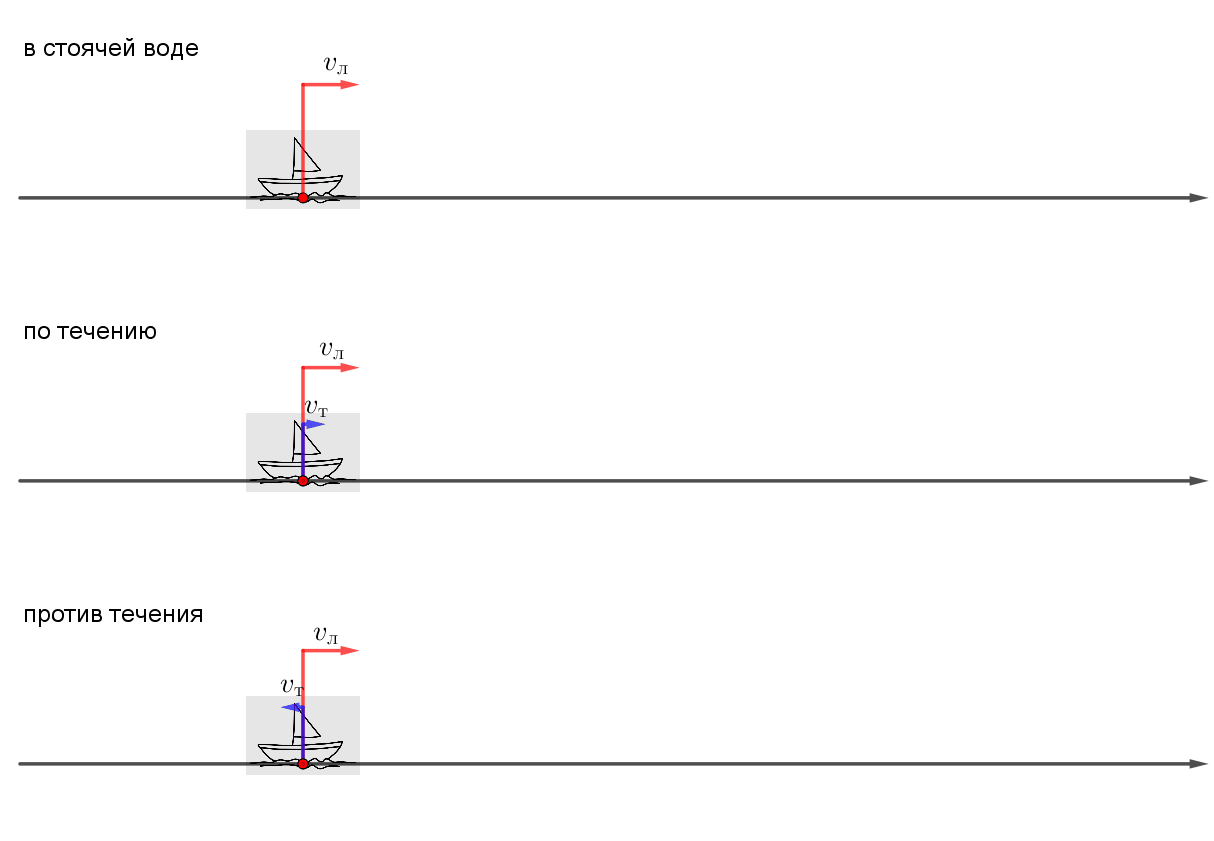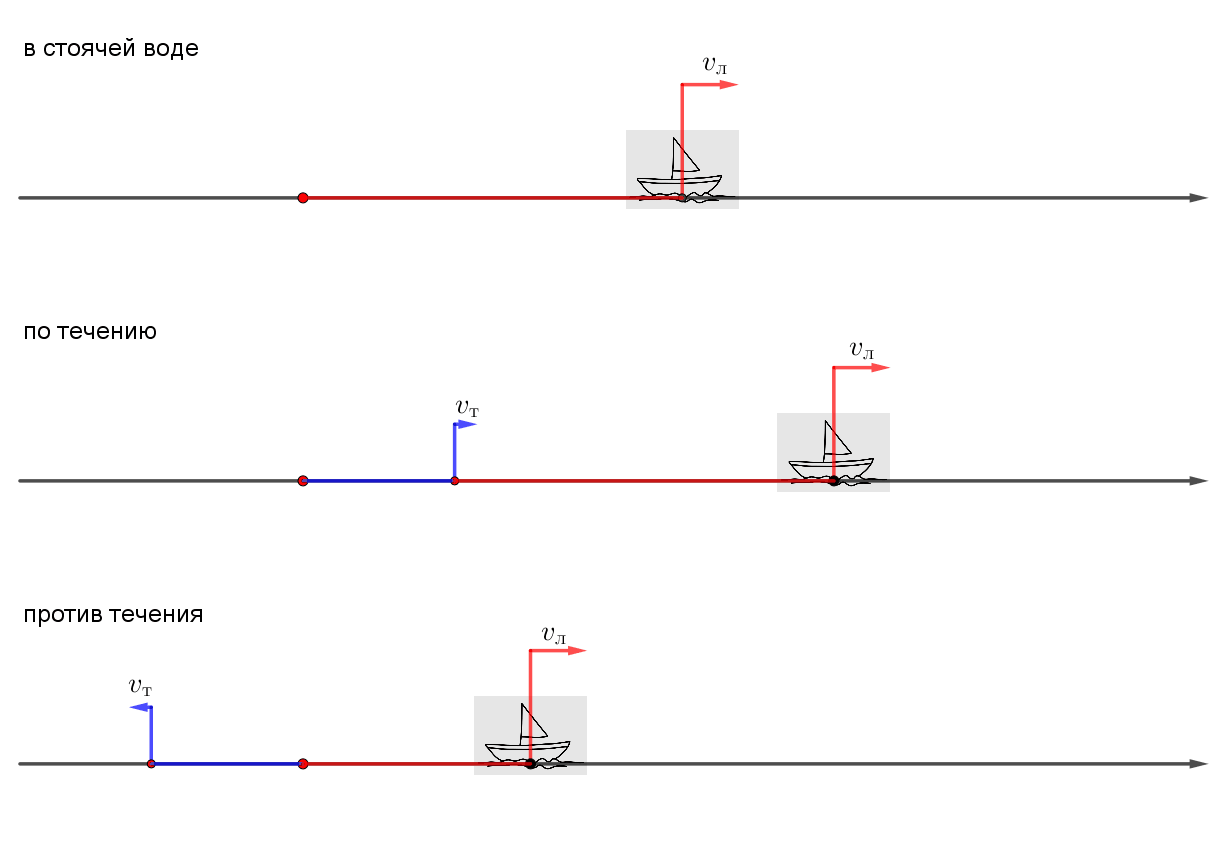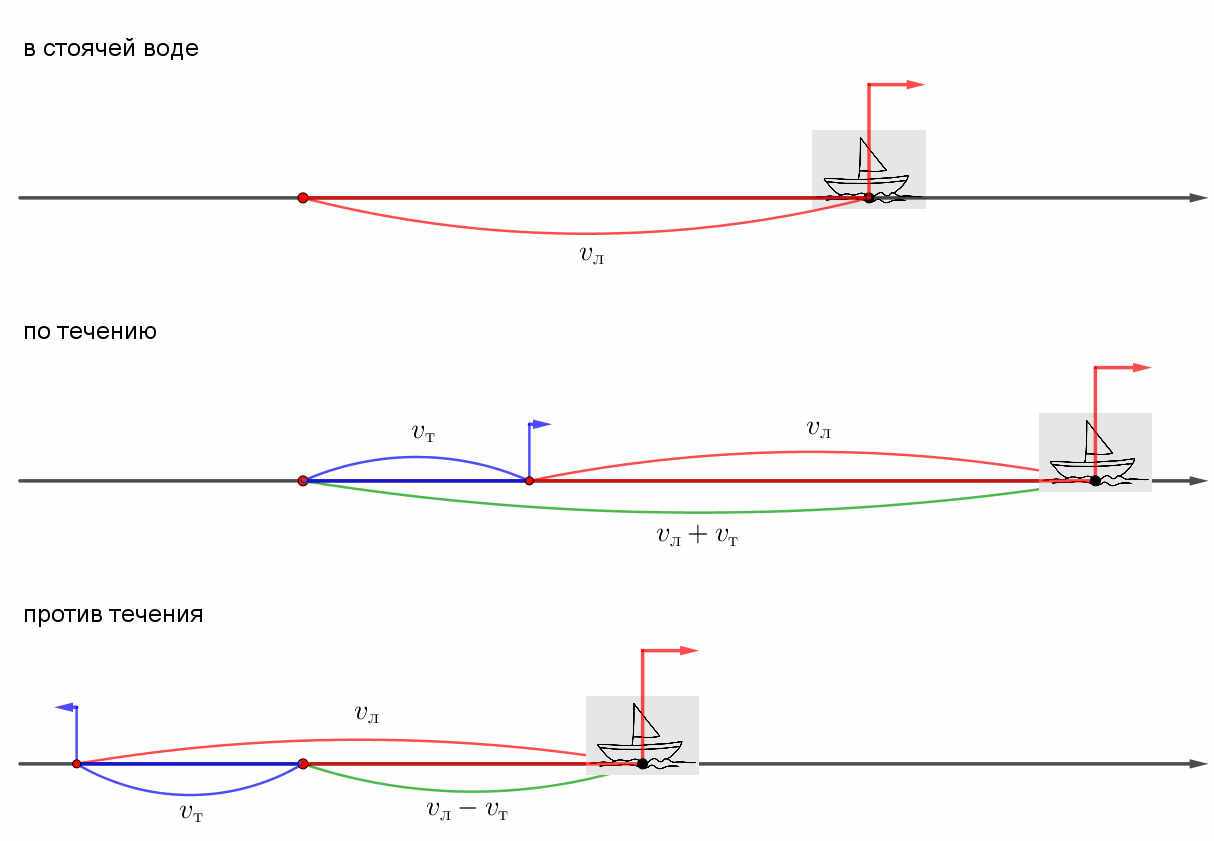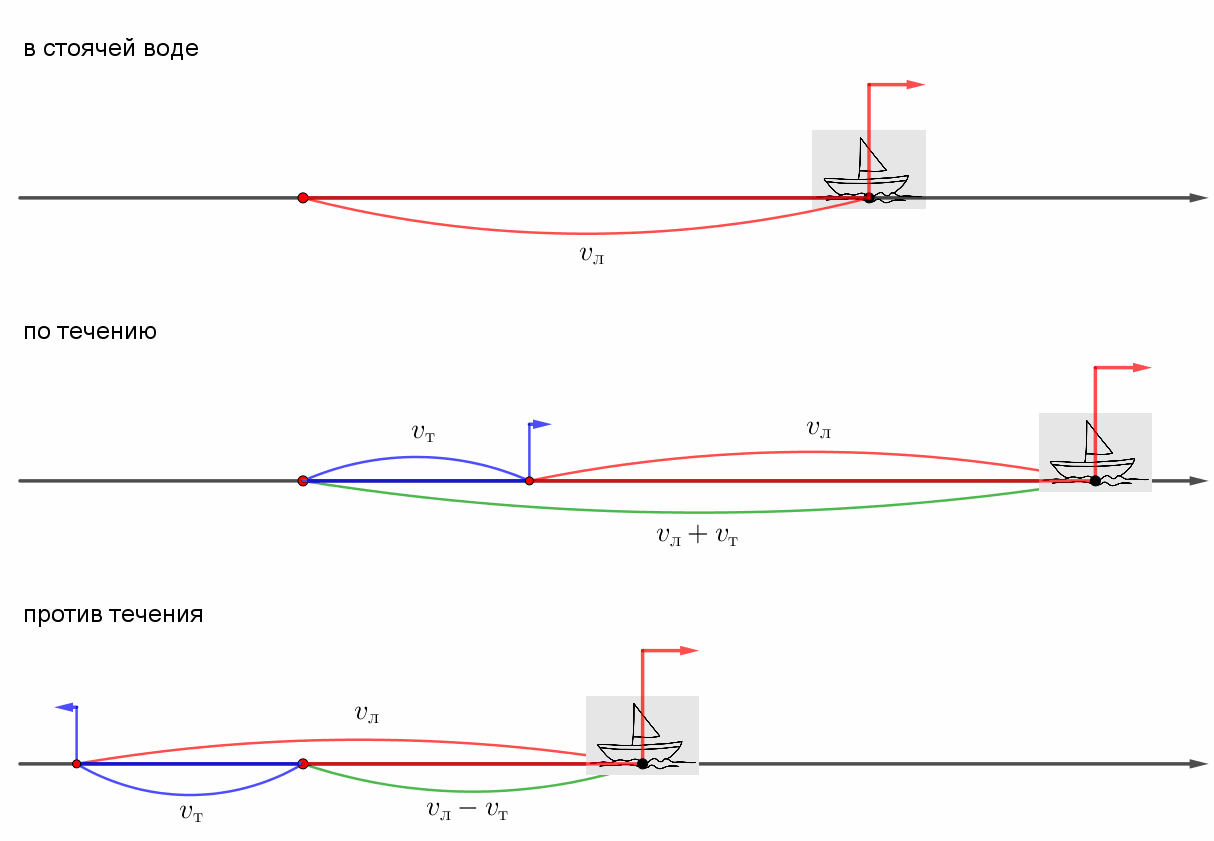
Если обозначить скорость движения лодки – \(\displaystyle v_л\) (в стоячей воде) и скорость течения – \(\displaystyle v_т\small,\) то

  • скорость движения лодки по течению равна: \(\displaystyle v_л+v_т\small,\)
  • скорость движения лодки против течения равна: \(\displaystyle v_л-v_т\small.\)

Подставляя скорость лодки \(\displaystyle v_л= 31{,}6\) км/ч и  скорость течения \(\displaystyle v_т=4{,}2\) км/ч, получаем:

\(\displaystyle v_{при\, \,движении\, \,против\, \,течения}=v_л-v_т=31{,}6-4{,}2=27{,}4\) км/ч

\(\displaystyle v_{при\, \,движении\, \,по\, \,течению}=v_л+v_т=31{,}6+4{,}2=35{,}8\) км/ч