Задание
км/ч
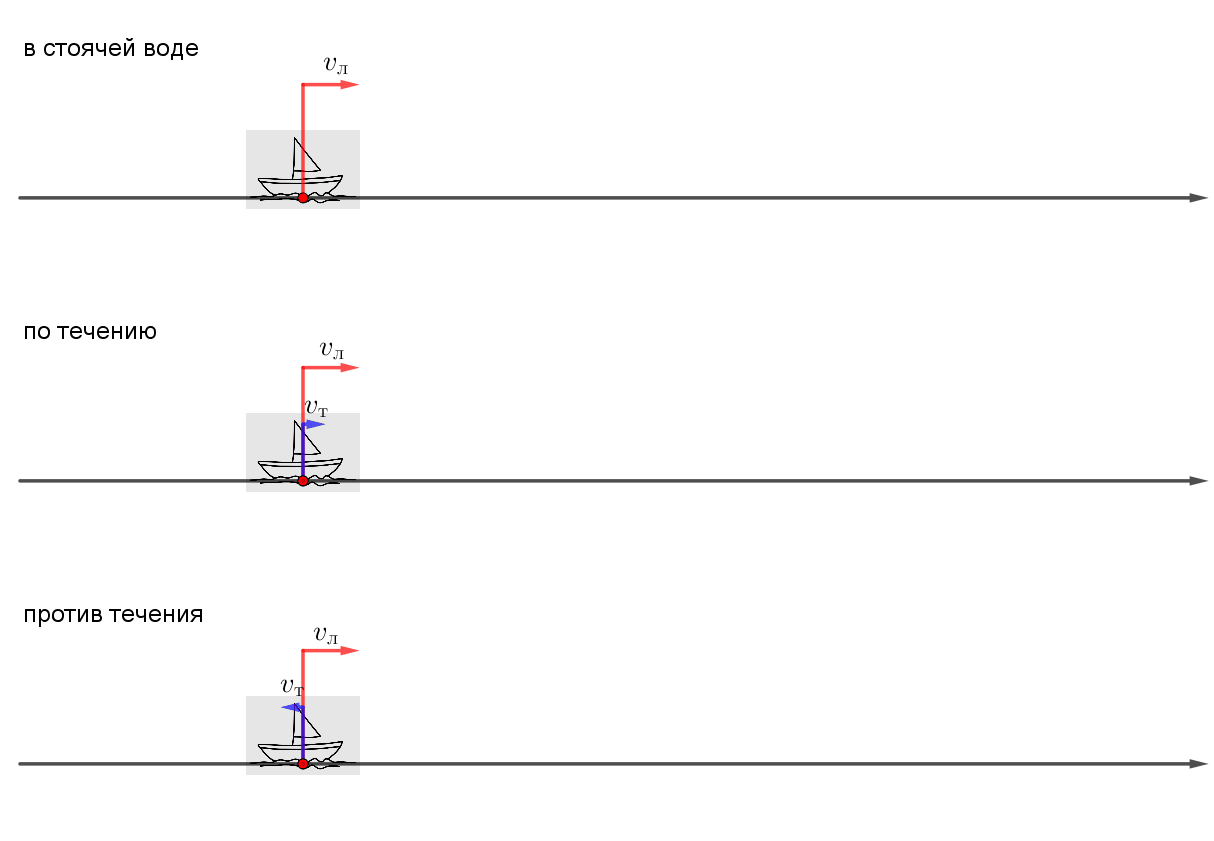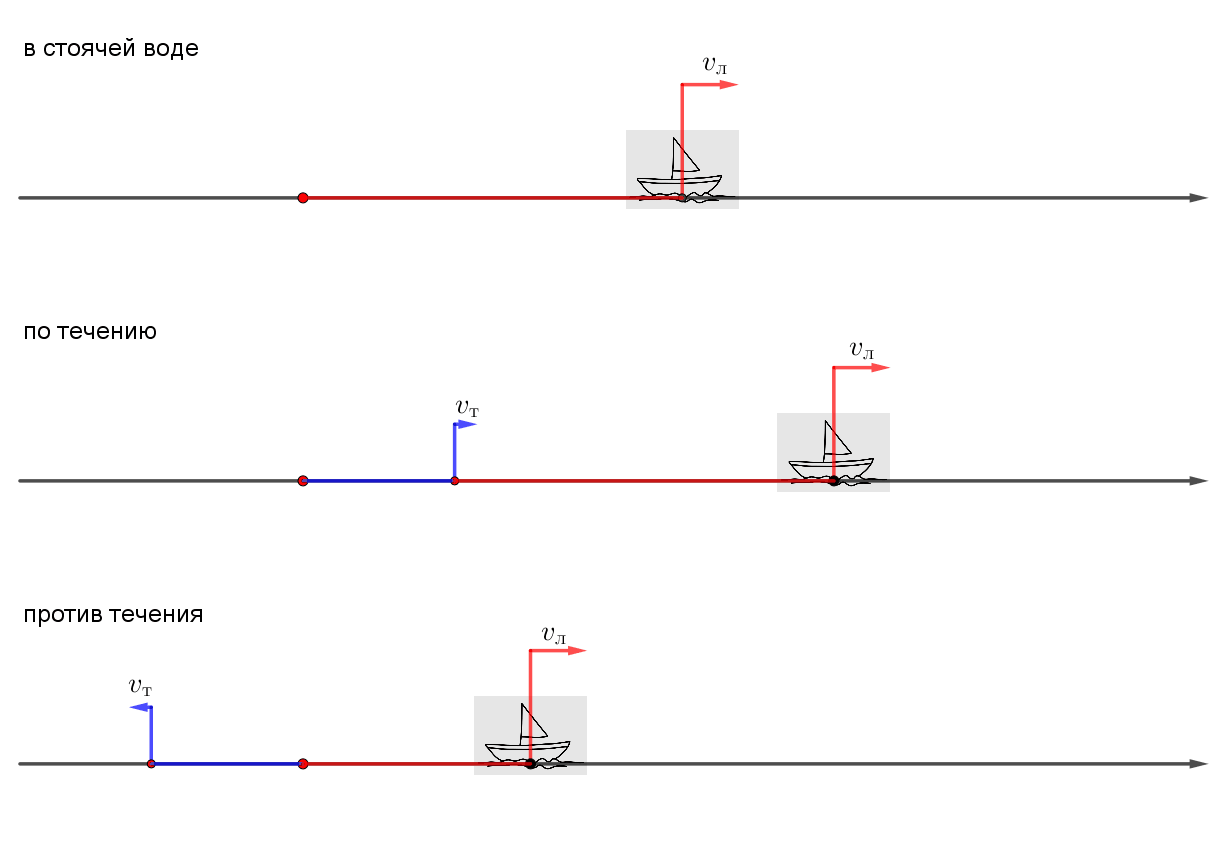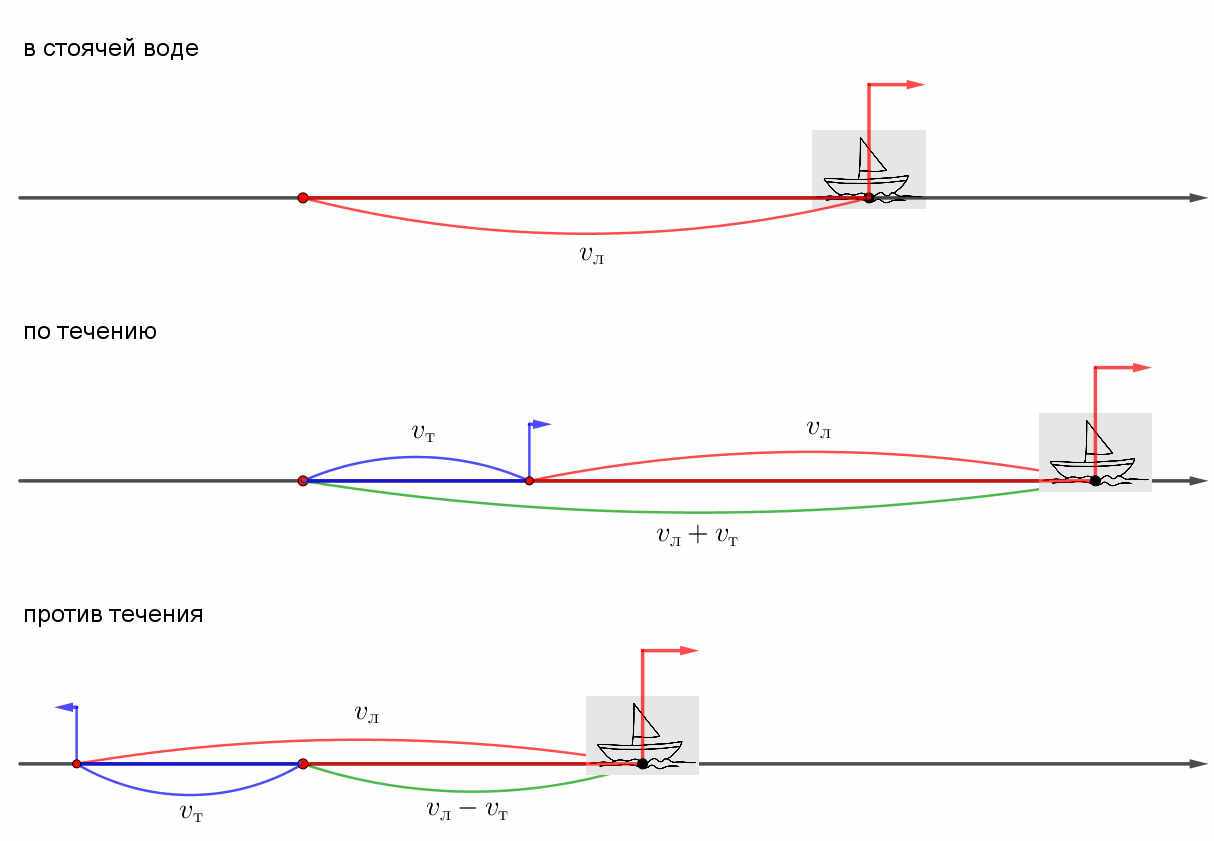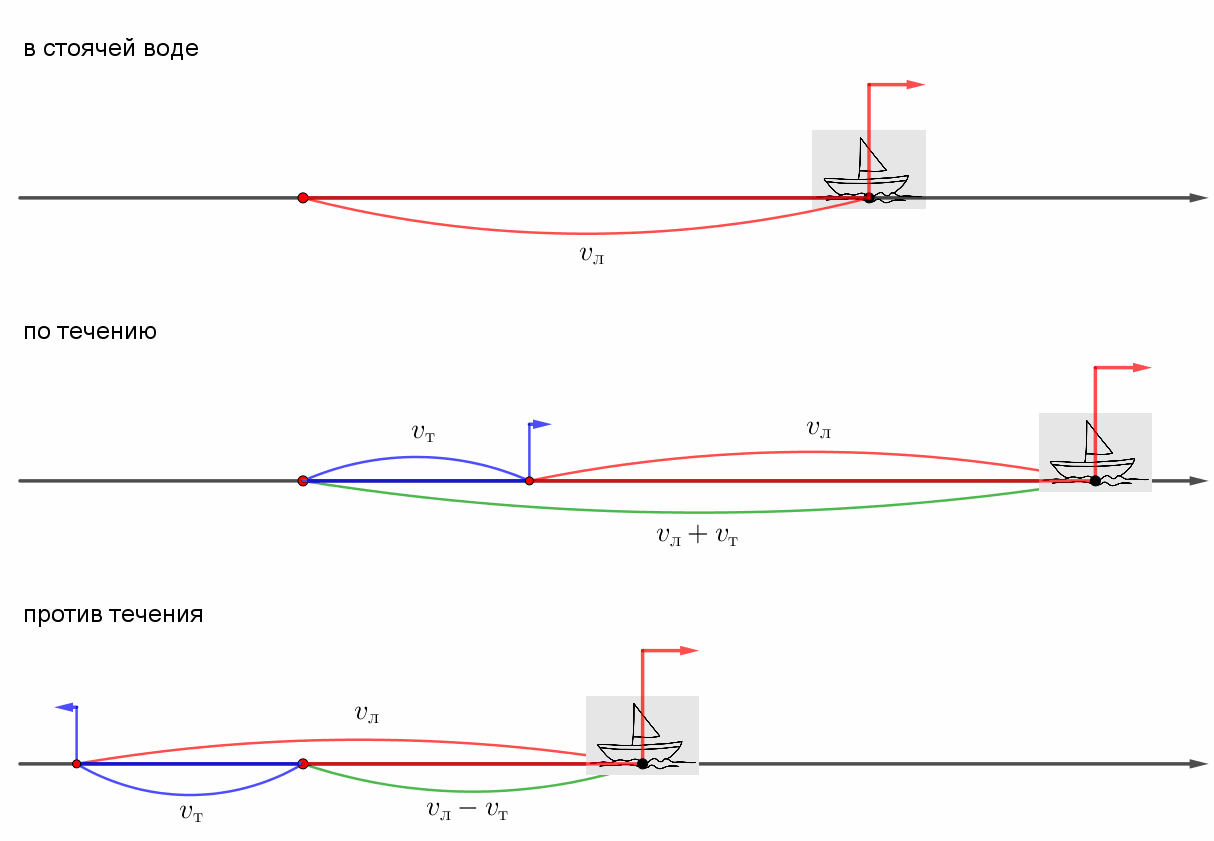
Моторная лодка, двигаясь по течению реки, прошла \(\displaystyle 156\) км за \(\displaystyle 5\) часов. Найдите собственную скорость лодки, если скорость течения реки равна \(\displaystyle 2{,}6\) км/ч.
Решение
Чтобы решить задачу:
- найдем скорость движения лодки при движении по течению,
- найдем собственную скорость лодки.
1. Двигаясь по течению, лодка прошла \(\displaystyle 156\) км за \(\displaystyle 5\) часов.
Тогда ее скорость при движении по течению равна
\(\displaystyle v_{по\,течению}=156:5=31{,}2\) км/ч.
2. Найдем собственную скорость лодки.
Если обозначить скорость движения лодки – \(\displaystyle v_л\) (в стоячей воде) и скорость течения – \(\displaystyle v_т\small,\) то
скорость движения лодки по течению равна: \(\displaystyle v_л+v_т\small.\)
Тогда собственная скорость лодки равна
\(\displaystyle v_л=v_{по\,течению}-v_т=31{,}2-2{,}6=28{,}6\) км/ч.
Ответ: \(\displaystyle 28{,}6\) км/ч.