Сколько хорд окружности показано на рисунке?

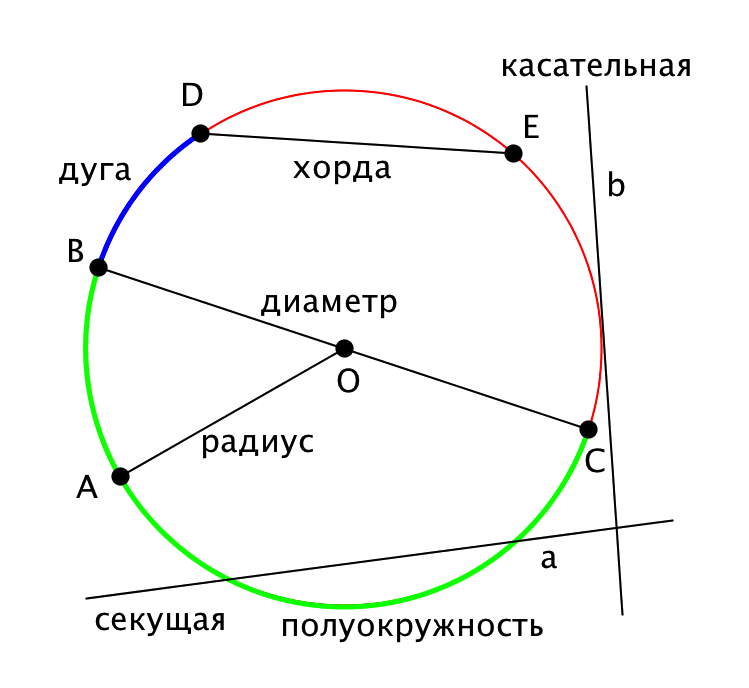
Отрезок, соединяющий центр окружности с любой из ее точек, называется ее радиусом.
Прямая, проходящая через любые две очки окружности, называется секущей.
Хорда - отрезок секущей, соединяющий две точки окружности (хорда - это отрезок, соединяющий две точки окружности).
Диаметр - хорда, проходящая через центр окружности.
Дуга - часть окружности.
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром.
Касательная - прямая, имеющая с окружностью только одну общую точку.
Перечислим отрезки, соединяющие две точки окружности, и подсчитаем их количество.

Отрезки: \(\displaystyle KL{\small ,}\) \(\displaystyle LM{\small ,}\) \(\displaystyle MN{\small ,}\) \(\displaystyle NK{\small ,}\) \(\displaystyle KM{\small ,}\) \(\displaystyle NL{\small .}\)
Их ровно \(\displaystyle 6{\small .}\)
Таким образом, на рисунке изображено \(\displaystyle 6\) хорд.
Ответ: \(\displaystyle 6\) хорд окружности.