На числовой прямой отмечено несколько точек и указаны координаты этих точек.
Опираясь на рисунок, расположите дроби в порядке возрастания:
Чтобы сравнить две дроби, можно посмотреть как они расположены на координатной прямой:
- дробь, которая на координатной прямой лежит правее – больше;
- дробь, которая на координатной прямой лежит левее – меньше.
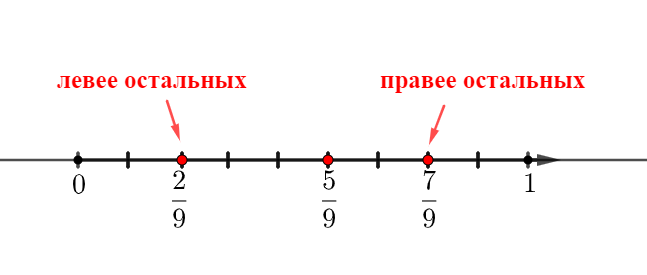
Дробь \(\displaystyle \frac{2}{9}\) расположена левее остальных на числовой прямой. Значит, она меньше остальных.
Дробь \(\displaystyle \frac{7}{9}\) расположена правее остальных на числовой прямой. Значит, она больше остальных.
Получаем:
\(\displaystyle \frac{2}{9} <\frac{5}{9} <\frac{7}{9} {\small .}\)