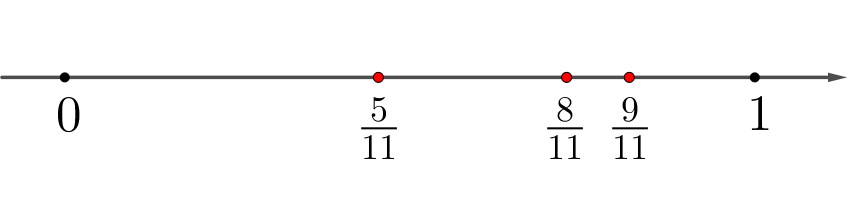
На числовой прямой отмечено несколько точек. Сопоставьте этим точкам их координаты:
Чтобы решить задачу:
- расположим дроби в порядке возрастания,
- сопоставим их соответствующим точкам на координатной прямой.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше:
\(\displaystyle \frac{\color{blue}{a}}{\color{green}{c}}>\frac{\color{blue}{b}}{\color{green}{c}}\small,\) если \(\displaystyle \color{blue}{a}>\color{blue}{b}\small.\)
У дробей \(\displaystyle \frac{\color{blue}{8}}{\color{green}{11}}{\small ,}\) \(\displaystyle \frac{\color{blue}{5}}{\color{green}{11}}\) и \(\displaystyle \frac{\color{blue}{9}}{\color{green}{11}}\) одинаковые знаменатели, равные \(\displaystyle \color{green}{11}\small.\) Сравним числители:
\(\displaystyle \color{blue}{5}<\color{blue}{8}<\color{blue}{9}{\small .}\)
Тогда
\(\displaystyle \frac{\color{blue}{5}}{11}<\frac{\color{blue}{8}}{11}<\frac{\color{blue}{9}}{11}{\small .}\)
Чтобы сравнить две дроби, можно посмотреть как они расположены на координатной прямой:
- дробь, которая на координатной прямой лежит правее – больше;
- дробь, которая на координатной прямой лежит левее – меньше.
Дробь \(\displaystyle \frac{5}{11}\) меньше остальных. Значит, она расположена левее остальных на координатной прямой.
Дробь \(\displaystyle \frac{9}{11}\) больше остальных. Значит, она расположена правее остальных на координатной прямой.
Таким образом, получаем