В бак налили воду, температура которой \(\displaystyle 10^{\circ}C{\small,}\) и нагревали её до \(\displaystyle 100^{\circ}C{\small,}\) причём через каждую минуту температура повышалась на \(\displaystyle 1{,}5^{\circ}C{\small.}\)
Зависимость температуры воды \(\displaystyle T\) (в градусах Цельсия) от времени нагревания \(\displaystyle t\) (в минутах)
задается формулой:
Постройте график этой зависимости.
(Двигайте синие точки на картинке)
| Пользуясь графиком, ответьте на вопросы. | Ответ: |
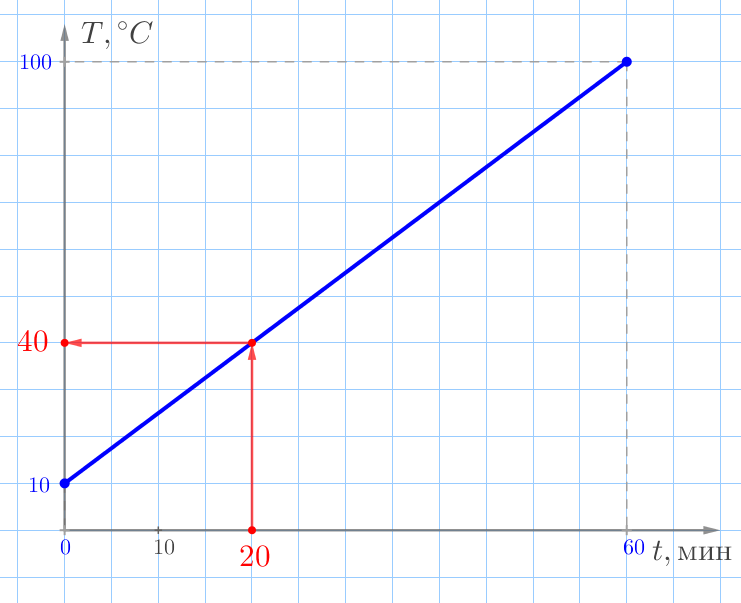
| \(\displaystyle 1)\) Какую температуру имела вода через \(\displaystyle 20\) минут после начала нагревания? | \(\displaystyle ^{\circ}C{\small.}\) |
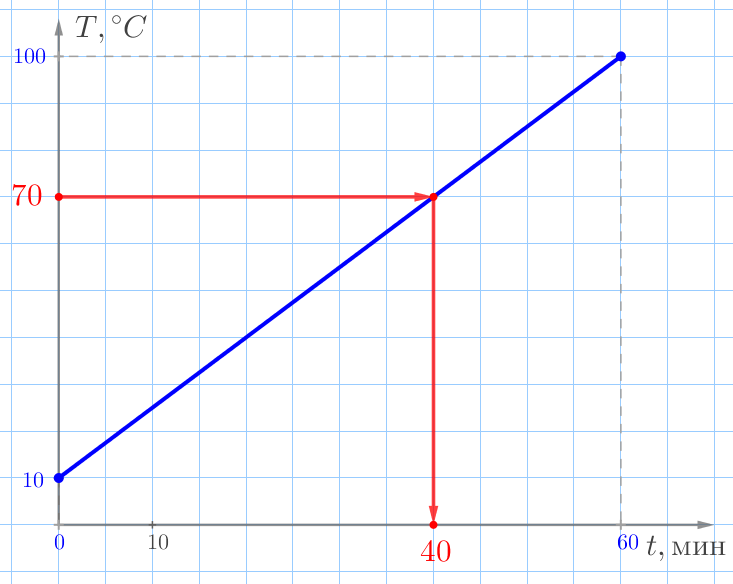
| \(\displaystyle 2)\) Через какое время вода нагрелась до \(\displaystyle 70^{\circ}C{\small?}\) | мин. |
\(\displaystyle \color{red}{1.}\) Зададим формулой зависимость температуры воды \(\displaystyle T\) от времени нагревания \(\displaystyle t{\small:}\)
\(\displaystyle T=10+1{,}5t\)
\(\displaystyle \color{red}{2.}\) Построим график зависимости, заданной формулой \(\displaystyle T=10+1{,}5t\)
при условии \(\displaystyle 10 \leq T \leq 100{\small.}\)
Графиком данной зависимости является отрезок с концами в точках
\(\displaystyle (0;10)\) и \(\displaystyle (60;100){\small.}\)
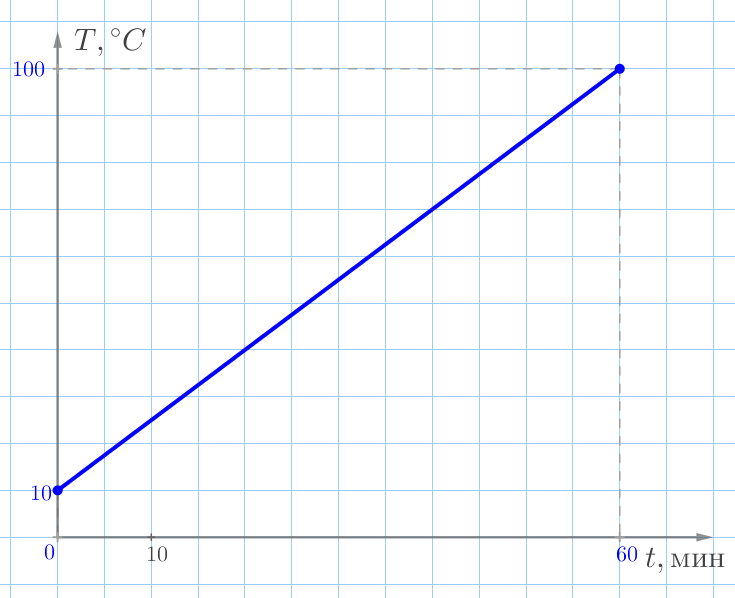
По горизонтальной прямой отмечается время в минутах, причём две клетки соответствуют десяти минутам. Значит, одна клетка соответствует пяти минутам:
\(\displaystyle 1\)клетка \(\displaystyle =5\)мин
По вертикальной прямой отмечается температура в градусах Цельсия, причём одной клетке соответствует десять градусов:
\(\displaystyle 1\)клетка \(\displaystyle =10^{\circ}C\)
\(\displaystyle \color{red}{3.}\) Пользуясь графиком, ответим на вопросы:
| Вопрос: | Ответ: |
| \(\displaystyle 1)\) Какую температуру имела вода через \(\displaystyle 20\) минут после начала нагревания? | \(\displaystyle 40^{\circ}C{\small.}\) |
| \(\displaystyle 2)\) Через какое время вода нагрелась до \(\displaystyle 70^{\circ}C{\small?}\) | \(\displaystyle 40\) мин. |