Задание
Длины трех сторон треугольника \(\displaystyle ABC\) равны \(\displaystyle 6{,}3\)см, \(\displaystyle 5{,}9\)см и \(\displaystyle 7{,}8\)см. Найдите сторону квадрата, который имеет такой же периметр, как треугольник \(\displaystyle ABC\small.\)
см
Решение
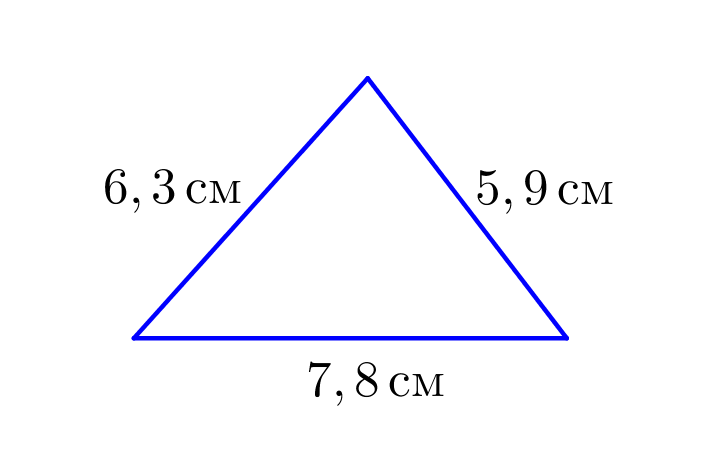
Периметр треугольника равен сумме длин его сторон, получаем:
\(\displaystyle \color{red}P_{треугольника}=7{,}8+5{,}9+6{,}3=20\)см.
Периметр квадрата равен периметру треугольника, то есть \(\displaystyle \color{red}P_{квадрата}=20\)см.
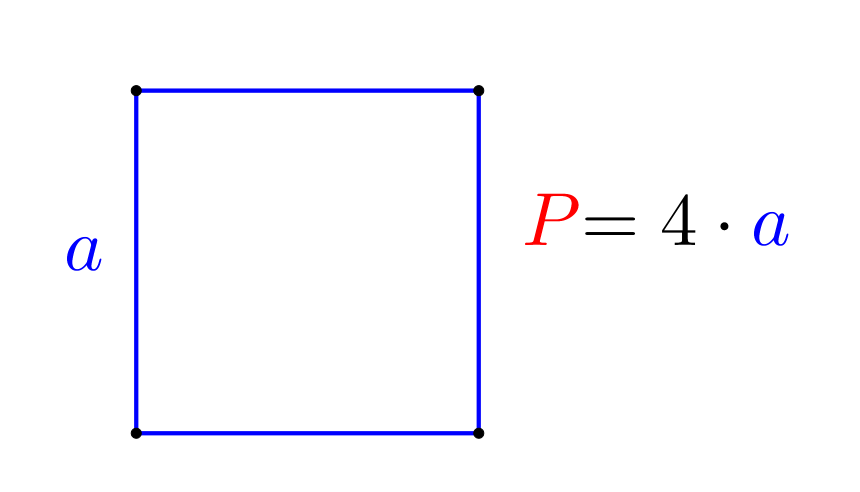
Длина стороны квадрата в \(\displaystyle 4\) раза меньше периметра и равна:
\(\displaystyle \color{blue}a=\color{red}P_{квадрата}:4=20:4=5\)см.
Ответ: \(\displaystyle 5\)см.