Используя линейку и транспортир, постройте в тетради треугольник \(\displaystyle ABC\small,\) у которого сторона \(\displaystyle BC\) равна \(\displaystyle 5\)см, угол \(\displaystyle B\) равен \(\displaystyle 40^{\circ}\small,\) угол \(\displaystyle C\) равен \(\displaystyle 80^{\circ}\small.\)
Измерьте транспортиром третий угол:
\(\displaystyle ^{\circ}\)
Что можно сказать про получившийся треугольник \(\displaystyle ABC?\)
(Выберите верный ответ из списка.)
Выполним необходимые построения.
1. Используя линейку, построим отрезок \(\displaystyle BC=5\)см:
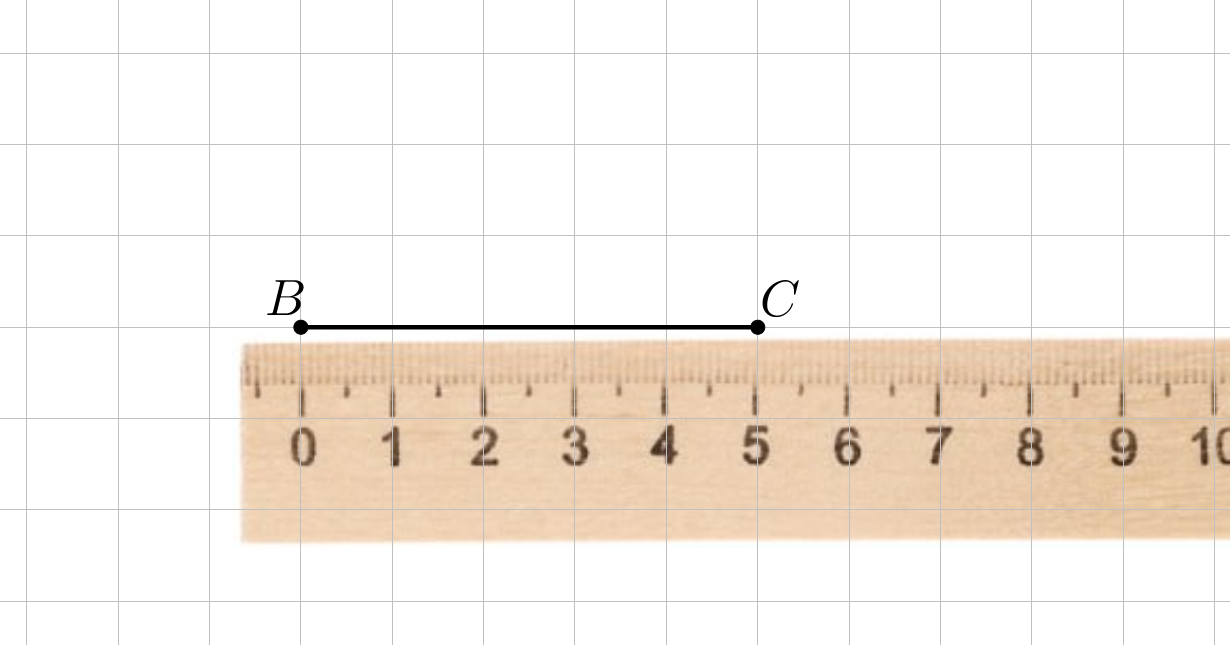
2. Используя транспортир, построим угол \(\displaystyle B\small,\) равный \(\displaystyle 40^{\circ}{\small:}\)
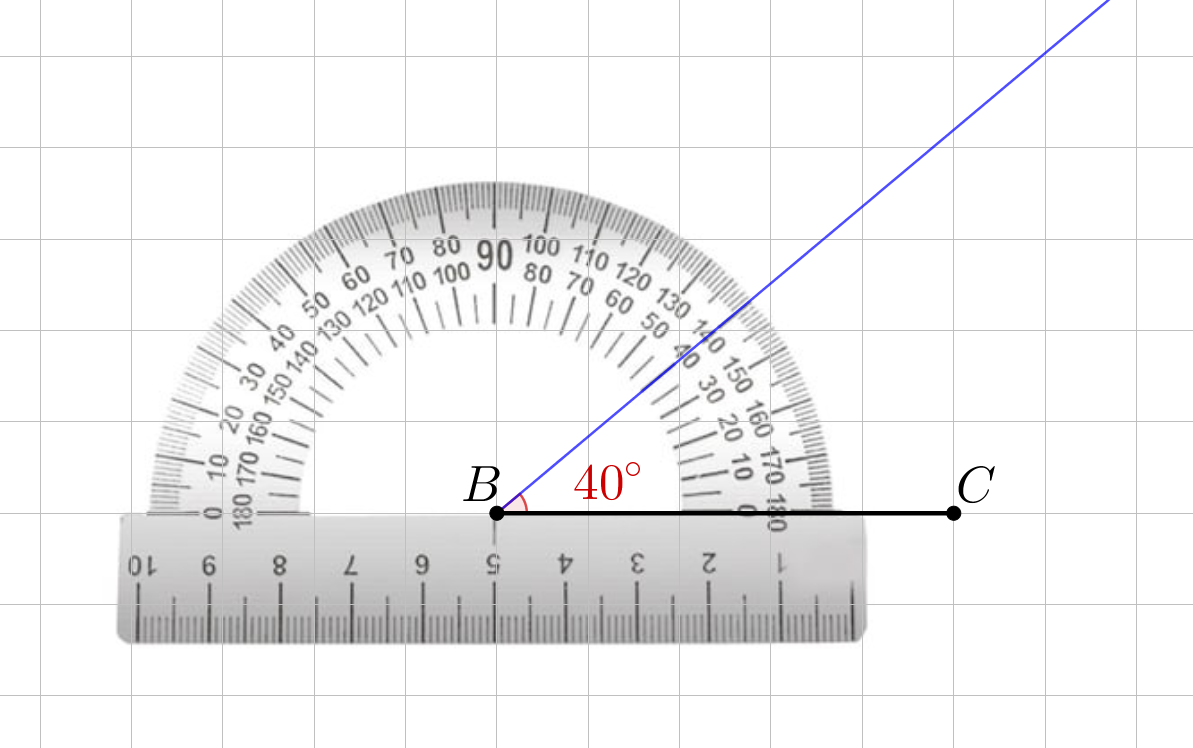
3. Используя транспортир, построим угол \(\displaystyle C\small,\) равный \(\displaystyle 80^{\circ}{\small,}\) и обозначим точку пересечения лучей буквой \(\displaystyle A\small:\)
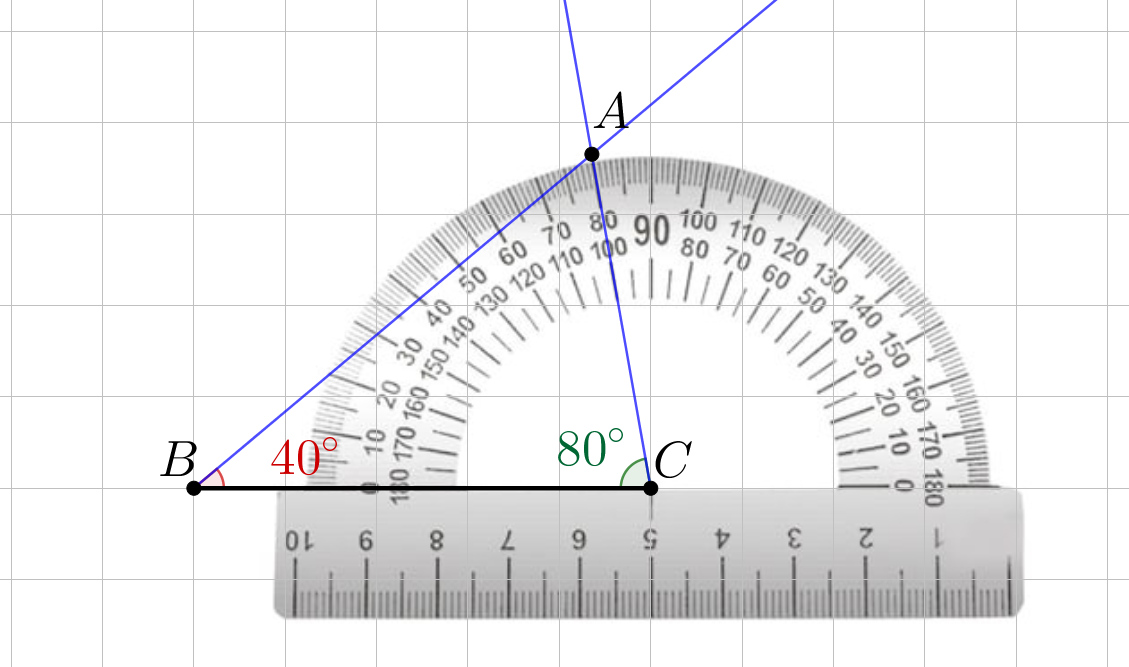
4. Используя транспортир, измерим угол \(\displaystyle A\small:\)
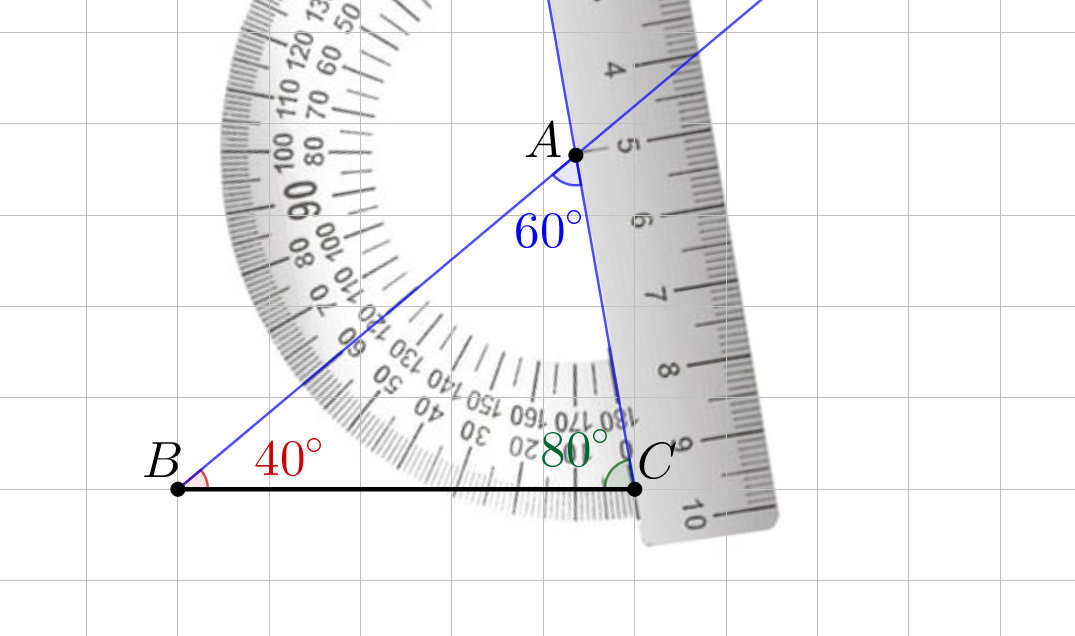
Получаем угол \(\displaystyle A\small,\) равный \(\displaystyle 60^{\circ}{\small.}\)
Получилось, что углы треугольника равны:
\(\displaystyle 40^{\circ},\,80^{\circ}\) и \(\displaystyle 60^{\circ}\small.\)
Ответ: угол \(\displaystyle A\) равен \(\displaystyle 60^{\circ}\) и треугольник \(\displaystyle ABC\) – остроугольный.