В выпуклом семиугольнике \(\displaystyle ABCDEFG\) проведите все диагонали из вершины \(\displaystyle A{\small.}\)
На сколько треугольников разделяют проведённые диагонали данный семиугольник?
Диагональ многоугольника – это отрезок, соединяющий любые две несоседние вершины многоугольника.
Две вершины многоугольника, принадлежащие одной стороне, называются соседними.
Проведём все диагонали из вершины \(\displaystyle A{\small,}\) то есть соединим вершину \(\displaystyle A\) со всеми несоседними вершинами.
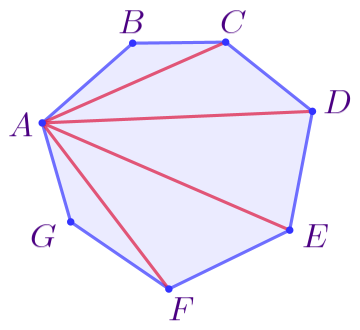
Проведённые диагонали разделили данный семиугольник на \(\displaystyle 5\) треугольников:
\(\displaystyle ABC{\small,}\) \(\displaystyle ACD{\small,}\) \(\displaystyle ADE{\small,}\) \(\displaystyle AEF{\small,}\) \(\displaystyle AFG{\small.}\)
Ответ: \(\displaystyle 5{\small.}\)
Если в выпуклом \(\displaystyle n\)–угольнике соединить диагоналями одну вершину со всеми несоседними вершинами, то проведённые диагонали разделят \(\displaystyle n\)–угольник на \(\displaystyle n-2\) треугольника.