Найдите стороны четырёхугольника \(\displaystyle ABCD{\small,}\) если его периметр равен \(\displaystyle 11{,}5\)см, а сторона \(\displaystyle AB\) меньше сторон \(\displaystyle BC{\small,}\) \(\displaystyle CD\) и \(\displaystyle AD\) соответственно на \(\displaystyle 4\)мм, \(\displaystyle 5\)мм и \(\displaystyle 6\)мм.
\(\displaystyle AB=\) см, \(\displaystyle BC=\) см, \(\displaystyle CD=\) см, \(\displaystyle AD=\) см.
Переведём все единицы в сантиметры:
\(\displaystyle 4\,{\footnotesize{мм}}=0{,}4\,{\footnotesize{см}}{\small;}\) \(\displaystyle 5\,{\footnotesize{мм}}=0{,}5\,{\footnotesize{см}}{\small;}\) \(\displaystyle 6\,{\footnotesize{мм}}=0{,}6\,{\footnotesize{см}}{\small.}\)
Пусть \(\displaystyle AB=x\)см. Тогда:
| 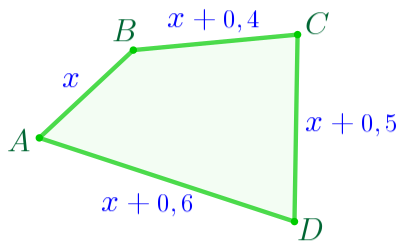 |
Периметр многоугольника равен сумме длин всех его сторон, значит:
\(\displaystyle P_{ABCD}=AB+BC+CD+AD{\small;} \)
\(\displaystyle 11{,}5=x+(x+0{,}4)+(x+0{,}5)+(x+0{,}6){\small.} \)
Решим полученное уравнение:
\(\displaystyle x+x+0{,}4+x+0{,}5+x+0{,}6=11{,}5{\small;} \)
\(\displaystyle 4x+1{,}5=11{,}5{\small;} \)
\(\displaystyle 4x=10{\small;} \)
\(\displaystyle x=2{,}5{\small.} \)
Найдем длины всех сторон:
- \(\displaystyle AB=2{,}5\,{\footnotesize{см}}{\small;}\)
- \(\displaystyle BC=2{,}5+0{,}4=2{,}9\,{\footnotesize{см}}{\small;}\)
- \(\displaystyle CD=2{,}5+0{,}5=3\,{\footnotesize{см}}{\small;}\)
- \(\displaystyle AD=2{,}5+0{,}6=3{,}1\,{\footnotesize{см}}{\small.}\)
Ответ: \(\displaystyle AB=2{,}5\,{\footnotesize{см}}{\small;}\) \(\displaystyle BC=2{,}9\,{\footnotesize{см}}{\small;}\) \(\displaystyle CD=3\,{\footnotesize{см}}{\small;}\) \(\displaystyle AD=3{,}1\,{\footnotesize{см}}{\small.}\)