Разрезать выпуклый многоугольник на треугольники.
ПРОИЗВОЛЬНОЕ РАЗРЕЗАНИЕ
Разрежем выпуклый многоугольник на треугольники произвольным образом:
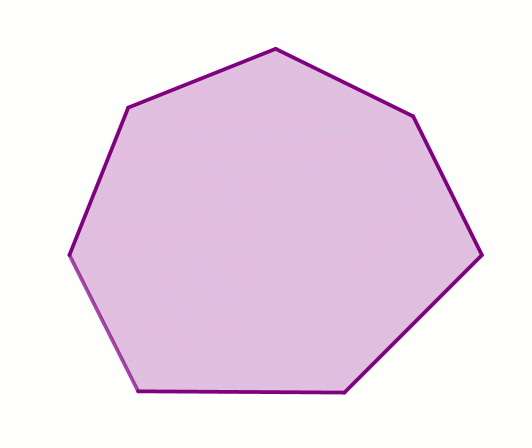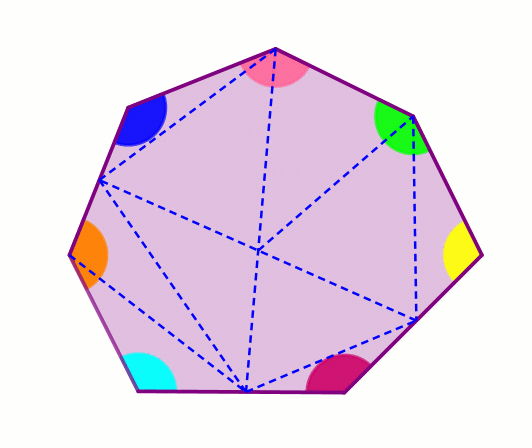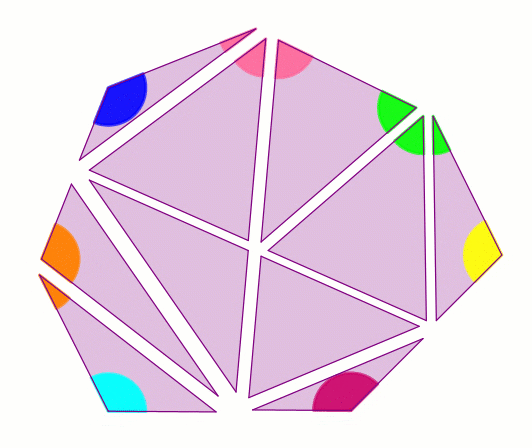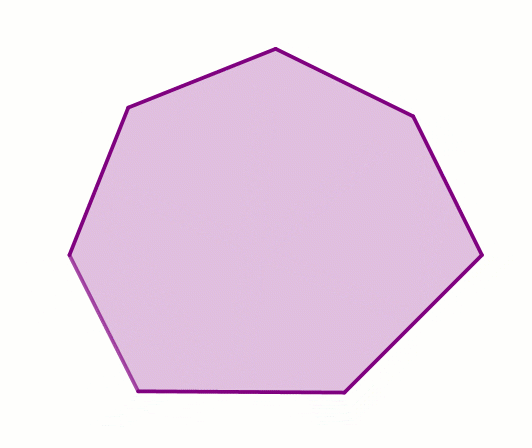
Заметим, что каждый угол исходного многоугольника является либо углом одного из полученных треугольников, либо суммой нескольких углов полученных треугольников.
Поэтому сумма углов многоугольника не больше суммы углов всех треугольников, полученных при разрезании.
РАЗРЕЗАНИЕ ПО ДИАГОНАЛЯМ
При разрезании выпуклого \(\displaystyle n\)–угольника на треугольники наименьшее количество треугольников получится, если резать многоугольник по непересекающимся диагоналям.
При этом:
- вершины треугольников – это точки, которые являются вершинами данного многоугольника,
- сумма всех углов полученных треугольников равна сумме внутренних углов данного многоугольника.
ПРИМЕР \(\displaystyle 1\)
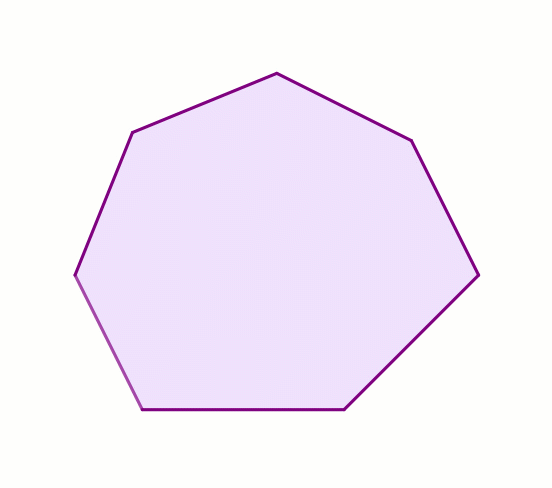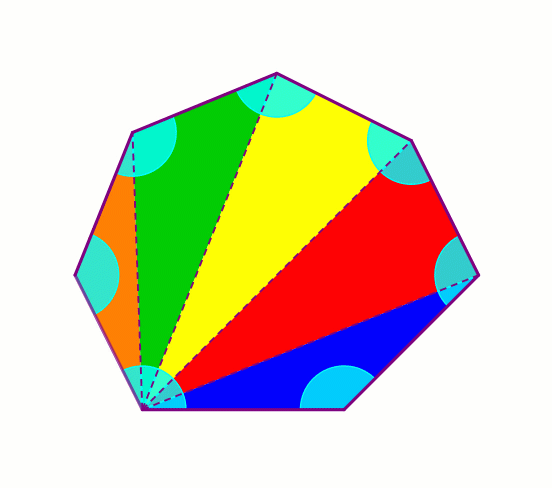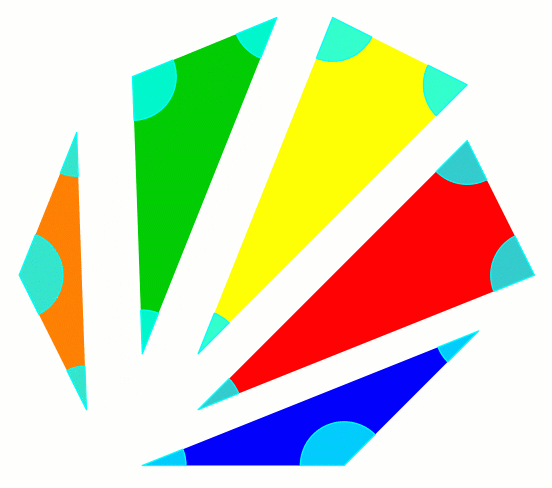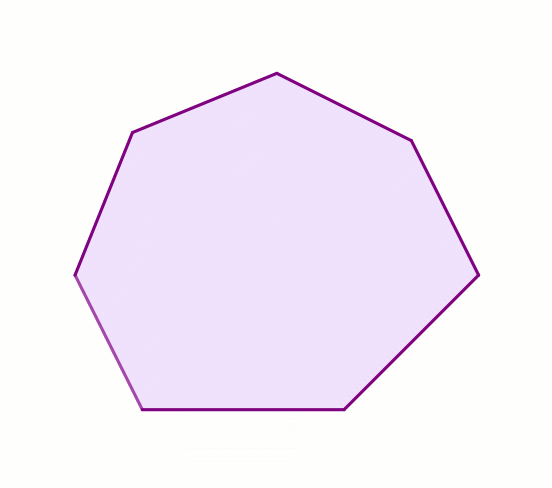
Разрежем выпуклый многоугольник произвольным образом по непересекающимся диагоналям.
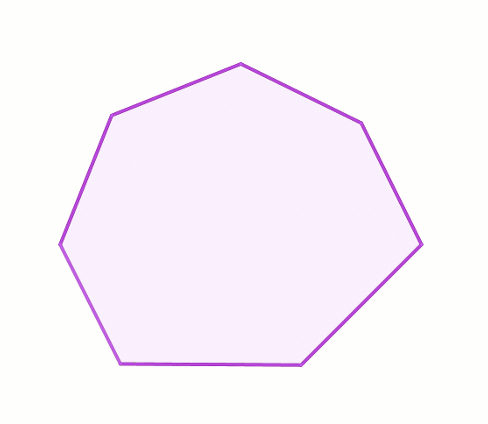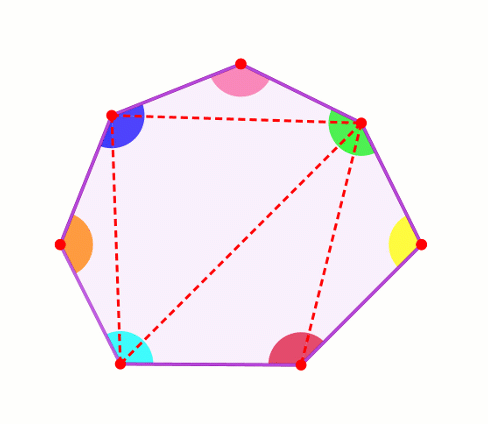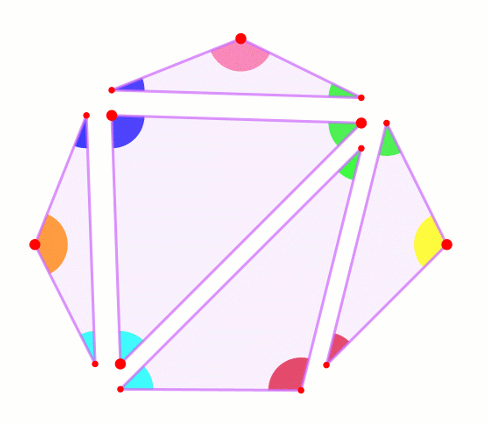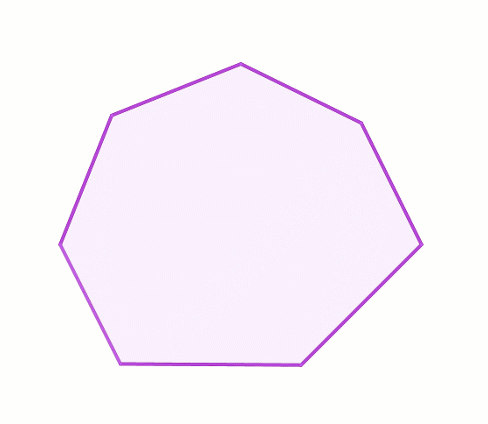
Заметим, что угол при каждой вершине многоугольника является либо углом одного из полученных треугольников, либо суммой нескольких углов полученных треугольников.
ПРИМЕР \(\displaystyle 2\)
Если в выпуклом \(\displaystyle n\)–угольнике соединить диагоналями одну вершину со всеми несоседними вершинами, то проведённые диагонали разделят \(\displaystyle n\)–угольник на \(\displaystyle n-2\) треугольника.