Можно ли выпуклый тридцатиугольник разрезать на \(\displaystyle 27\) треугольников?
При разрезании выпуклого многоугольника на треугольники сумма углов всех полученных треугольников не может оказаться меньше суммы углов исходного многоугольника.
Разрежем выпуклый многоугольник на треугольники произвольным образом:
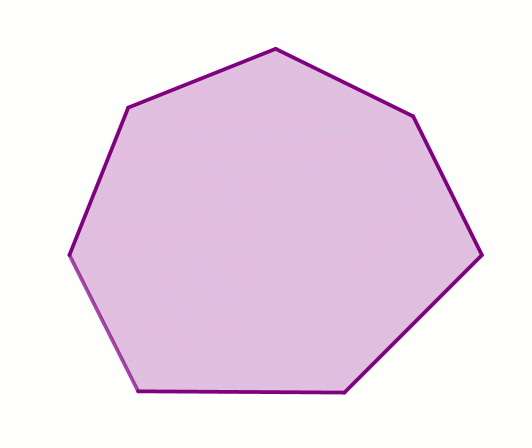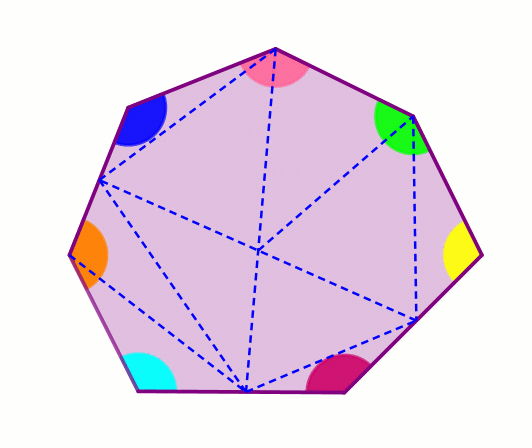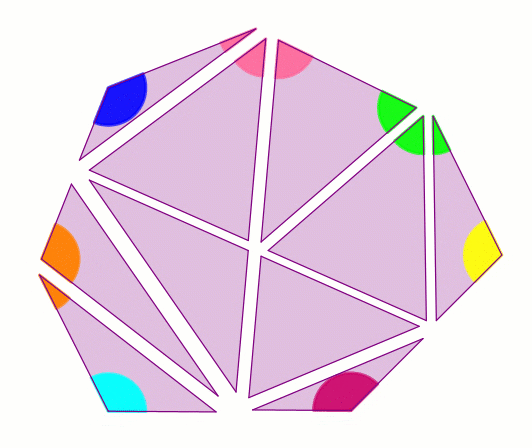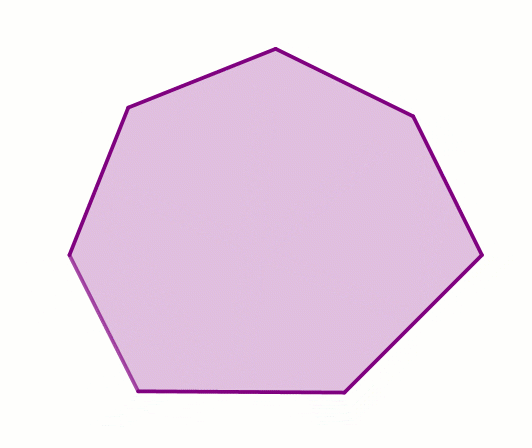
Заметим, что каждый угол исходного многоугольника является либо углом одного из полученных треугольников, либо суммой нескольких углов полученных треугольников.
Поэтому сумма углов многоугольника не больше суммы углов всех треугольников, полученных при разрезании.
Сумма углов выпуклого тридцатиугольника равна
\(\displaystyle S_{30}=180^{\circ}\cdot (30-2) =180^{\circ}\cdot 28{\small.}\)
Значит, при разрезании выпуклого тридцатиугольника на треугольники сумма углов всех полученных треугольников не может быть меньше \(\displaystyle 180^{\circ}\cdot 28{\small.}\)
Но сумма углов \(\displaystyle 27\) треугольников равна \(\displaystyle 180^{\circ}\cdot 27{\small,}\) то есть меньше чем \(\displaystyle 180^{\circ}\cdot 28{\small.}\)
Следовательно, выпуклый тридцатиугольник нельзя разрезать на \(\displaystyle 27\) треугольников.
Ответ: Нет.