Найдите сумму внешних углов выпуклого шестиугольника.
Ответ дайте в градусах.
\(\displaystyle ^{\circ}\)
| Внешним углом выпуклого многоугольника называется угол, смежный с углом многоугольника. | 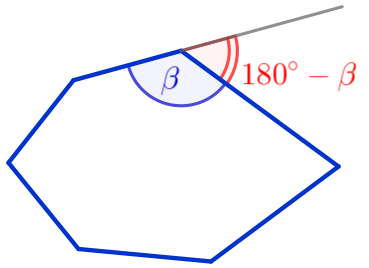 |
Построим выпуклый шестиугольник \(\displaystyle \color{blue}{A_1A_2A_3A_4A_5A_6}\).
Найдём сумму его внешних углов.
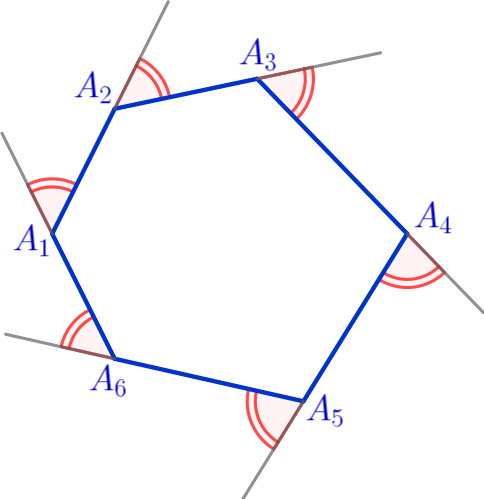
Пусть \(\displaystyle \color{green}{\alpha_1}{\small,}\) \(\displaystyle \color{green}{\alpha_2}{\small,}\) \(\displaystyle \color{green}{\alpha_3}{\small,}\) \(\displaystyle \color{green}{\alpha_4}{\small,}\) \(\displaystyle \color{green}{\alpha_5}{\small,}\) \(\displaystyle \color{green}{\alpha_6}\) – углы данного шестиугольника.
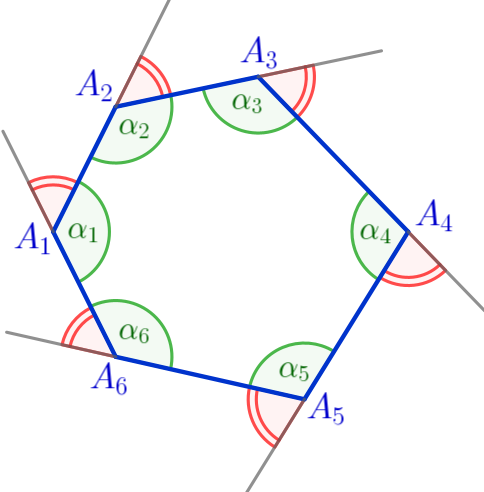
Сумма углов выпуклого \(\displaystyle n\)–угольника вычисляется по формуле:
\(\displaystyle S_n=180^{\circ}\cdot (n-2) {\small.}\)
Значит,
\(\displaystyle S_6=\color{green}{\alpha_1}+\color{green}{\alpha_2}+\color{green}{\alpha_3}+\color{green}{\alpha_4}+\color{green}{\alpha_5}+\color{green}{\alpha_6}=180^{\circ} \cdot (6-2)=180^{\circ} \cdot 4{\small.} \)
Тогда сумма внешних углов шестиугольника \(\displaystyle \color{blue}{A_1A_2A_3A_4A_5A_6}\) равна:
\(\displaystyle\begin{aligned}(180^{\circ}-\color{green}{\alpha_1})&+(180^{\circ}-\color{green}{\alpha_2})+(180^{\circ}-\color{green}{\alpha_3})+(180^{\circ}-\color{green}{\alpha_4})+(180^{\circ}-\color{green}{\alpha_5})+(180^{\circ}-\color{green}{\alpha_6})=\\ \\&=180^{\circ} \cdot 6-(\color{green}{\alpha_1}+\color{green}{\alpha_2}+\color{green}{\alpha_3}+\color{green}{\alpha_4}+\color{green}{\alpha_5}+\color{green}{\alpha_6})=\\ \\&=180^{\circ} \cdot 6-180^{\circ} \cdot 4=180^{\circ} \cdot (6-4)=180^{\circ} \cdot 2=360^{\circ}{\small.}\end{aligned}\)
Ответ: \(\displaystyle 360^{\circ}{\small.}\)
Сумма внешних углов выпуклого \(\displaystyle n\)–угольника равна \(\displaystyle 360^{\circ}{\small.}\)