В выпуклом четырёхугольнике \(\displaystyle ABCD\) биссектрисы углов \(\displaystyle B\) и \(\displaystyle D\) пересекаются в точке \(\displaystyle O{\small.}\)
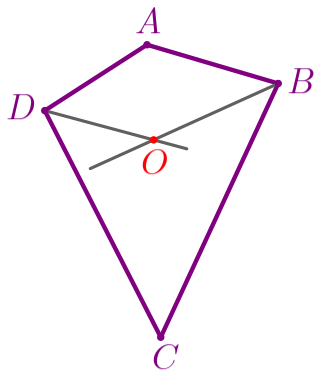
Найдите угол \(\displaystyle BOD{\small,}\) если \(\displaystyle \angle A=130^{\circ}{\small,}\) \(\displaystyle \angle C=50^{\circ}{\small.}\)
\(\displaystyle \angle BOD=\) \(\displaystyle ^{\circ}\)
Обозначим на рисунке:
| 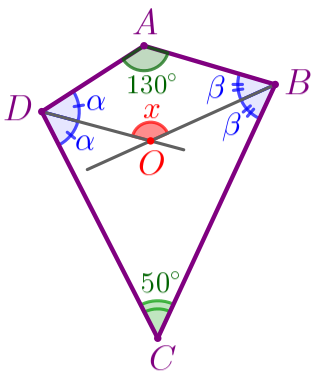 |
Рассмотрим четырёхугольник \(\displaystyle ABOD{\small.}\)
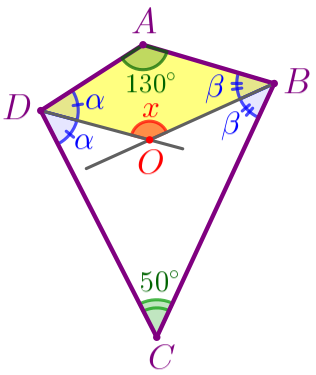 | В выпуклом четырёхугольнике \(\displaystyle ABOD{\small:}\) \(\displaystyle \angle A+\angle B+\angle O+\angle D=360^{\circ}{\small.} \) То есть \(\displaystyle \color{green}{130^{\circ}}+\color{blue}{\beta}+ \color{red}{x}+\color{blue}{\alpha}=360^{\circ}{\small.} \) Получаем: \(\displaystyle \color{red}{x}=360^{\circ}-\color{green}{130^{\circ}}-(\color{blue}{\alpha}+\color{blue}{\beta}){\small;} \) \(\displaystyle \color{red}{x}=230^{\circ}-(\color{blue}{\alpha}+\color{blue}{\beta}){\small.} \) |
Найдем сумму \(\displaystyle (\color{blue}{\alpha}+\color{blue}{\beta}){\small.} \)
В выпуклом четырёхугольнике \(\displaystyle ABCD{\small:}\) \(\displaystyle \angle A+\angle B+\angle C+\angle D=360^{\circ}{\small.} \) То есть \(\displaystyle \color{green}{130^{\circ}}+2\color{blue}{\beta}+\color{green}{50^{\circ}}+2\color{blue}{\alpha}=360^{\circ}{\small.} \) Получаем: \(\displaystyle 2(\color{blue}{\alpha}+\color{blue}{\beta})=360^{\circ}-\color{green}{130^{\circ}}-\color{green}{50^{\circ}}{\small;} \) \(\displaystyle 2(\color{blue}{\alpha}+\color{blue}{\beta})=180^{\circ}{\small;} \) \(\displaystyle \color{blue}{\alpha}+\color{blue}{\beta}=90^{\circ}{\small.} \) | 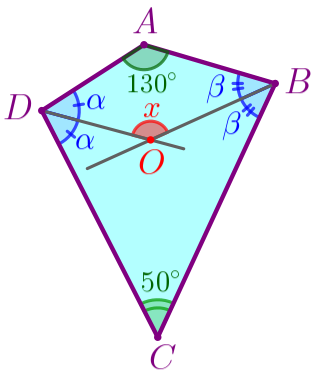 |
Найдем значение \(\displaystyle \color{red}{x}{\small:}\)
\(\displaystyle \color{red}{x}=230^{\circ}-(\color{blue}{\alpha}+\color{blue}{\beta}){\small;} \)
\(\displaystyle \color{red}{x}=230^{\circ}-90^{\circ}=140^{\circ}{\small.} \)
Значит,
\(\displaystyle \angle BOD=140^{\circ}{\small.}\)
Ответ: \(\displaystyle 140^{\circ}{\small.}\)