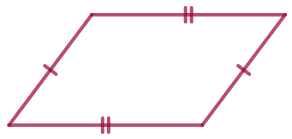
В четырёхугольнике \(\displaystyle ABCD\) стороны \(\displaystyle AB\) и \(\displaystyle CD\) параллельны, диагонали \(\displaystyle AC\) и \(\displaystyle BD\) пересекаются в точке \(\displaystyle O{\small,}\) \(\displaystyle AO=7{\small,}\) \(\displaystyle BC=12{\small,}\) \(\displaystyle OC=7{\small.}\) Найдите сторону \(\displaystyle AD{\small.}\)
\(\displaystyle AD=\)
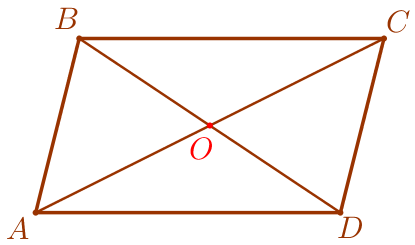
\(\displaystyle ABCD\) – четырёхугольник:
Требуется найти сторону \(\displaystyle AD{\small.}\) | 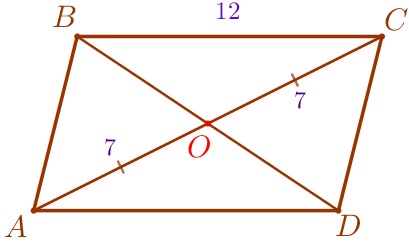 |
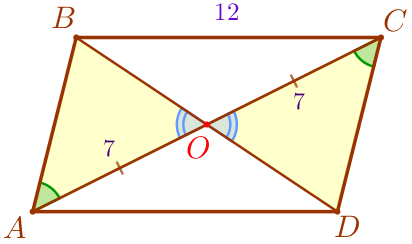 | \(\displaystyle \triangle AOB = \triangle COD\) по стороне и двум прилежащим углам:
|
В результате получаем
\(\displaystyle BO=OD{\small.}\)
Признак параллелограмма
 | Если диагонали четырёхугольника делятся точкой пересечения пополам, то он является параллелограммом. |
Поскольку \(\displaystyle AO=OC\) и \(\displaystyle BO=OD{\small,}\) то диагонали четырёхугольника \(\displaystyle ABCD\) делятся точкой пересечения пополам. Значит, \(\displaystyle ABCD\) – параллелограмм. | 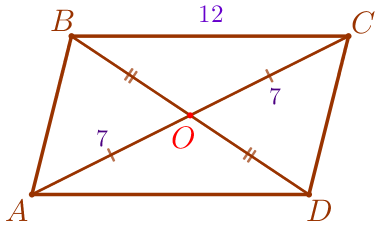 |
\(\displaystyle AD=BC=12{\small.}\)
Ответ: \(\displaystyle AD=12{\small.}\)