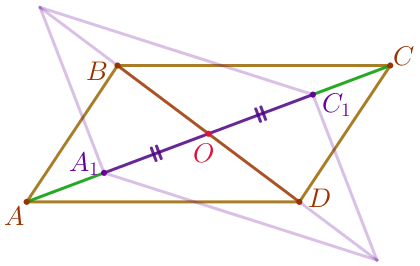
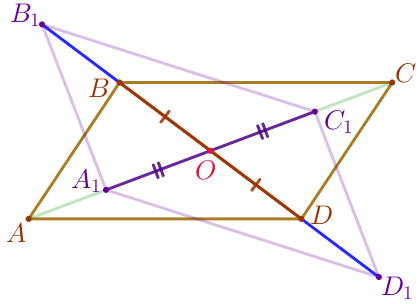
В параллелограмме \(\displaystyle ABCD\) на диагонали \(\displaystyle AC\) отмечены точки \(\displaystyle A_1\) и \(\displaystyle C_1\) так, что \(\displaystyle AA_1=CC_1{\small.}\) На продолжении диагонали \(\displaystyle BD\) за точку \(\displaystyle B\) отмечена точка \(\displaystyle B_1{\small,}\) а на продолжении этой диагонали за точку \(\displaystyle D\) отмечена точка \(\displaystyle D_1\) так, что \(\displaystyle BB_1=DD_1{\small.}\)
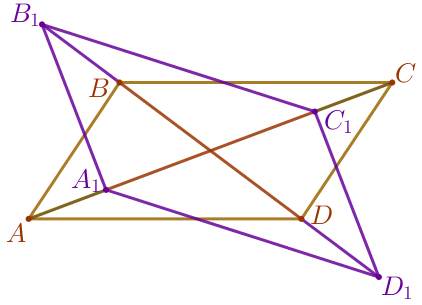
Является ли четырёхугольник \(\displaystyle A_1B_1C_1D_1\) параллелограммом?
Почему?
 | Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам. |
Обозначим точку пересечения диагоналей \(\displaystyle AC\) и \(\displaystyle BD\) параллелограмма \(\displaystyle ABCD\) буквой \(\displaystyle \color{red}{O}{\small.}\)
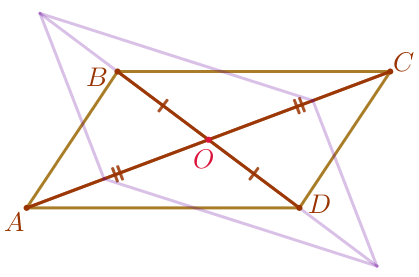 | По свойству параллелограмма точка \(\displaystyle \color{red}{O}\) делит каждую диагональ параллелограмма \(\displaystyle ABCD\) пополам, то есть \(\displaystyle \color{brown}{AO}=\color{brown}{OC}{\small,}\) \(\displaystyle \color{brown}{BO}=\color{brown}{OD}{\small.}\) |
Точки \(\displaystyle A_1\) и \(\displaystyle C_1\) отмечены на диагонали \(\displaystyle AC\) так, что \(\displaystyle \color{green}{AA_1}=\color{green}{CC_1}{\small.}\) Тогда \(\displaystyle \color{darkviolet}{A_1O}=\color{brown}{AO}-\color{green}{AA_1}{\small,}\) \(\displaystyle \color{darkviolet}{OC_1}=\color{brown}{OC}-\color{green}{CC_1}{\small.}\) Разности соответственно равных отрезков равны. Значит, \(\displaystyle \color{darkviolet}{A_1O}=\color{darkviolet}{OC_1}{\small.}\) |
|
Точки \(\displaystyle B_1\) и \(\displaystyle D_1\) отмечены на продолжении диагонали \(\displaystyle BD\) так, что \(\displaystyle \color{blue}{BB_1}=\color{blue}{DD_1}{\small.}\) Тогда \(\displaystyle \color{darkviolet}{B_1O}=\color{brown}{BO}+\color{blue}{BB_1}{\small,}\) \(\displaystyle \color{darkviolet}{OD_1}=\color{brown}{OD}+\color{blue}{DD_1}{\small.}\) Суммы соответственно равных отрезков равны. Значит, \(\displaystyle \color{darkviolet}{B_1O}=\color{darkviolet}{OD_1}{\small.}\) |
|
Рассмотрим четырёхугольник \(\displaystyle A_1B_1C_1D_1{\small:}\)
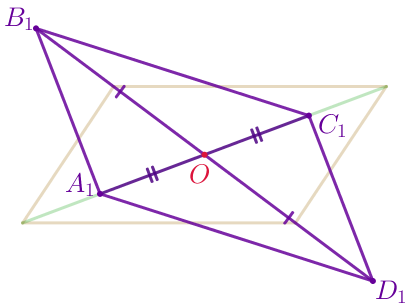 | Диагонали \(\displaystyle A_1C_1\) и \(\displaystyle B_1C_1\) четырёхугольника \(\displaystyle A_1B_1C_1D_1\) пересекаются в точке \(\displaystyle \color{red}{O}\) так, что \(\displaystyle \color{darkviolet}{A_1O}=\color{darkviolet}{OC_1}{\small,}\) \(\displaystyle \color{darkviolet}{B_1O}=\color{darkviolet}{OD_1}{\small.}\) То есть диагонали данного четырёхугольника точкой пересечения делятся пополам. |
 | Если диагонали четырёхугольника делятся точкой пересечения пополам, то он является параллелограммом. |
Следовательно,
\(\displaystyle A_1B_1C_1D_1\) – параллелограмм.
| Ответ: | Является ли четырёхугольник \(\displaystyle A_1B_1C_1D_1\) параллелограммом? Да. Почему? Диагонали точкой пересечения делятся пополам. |