Стороны треугольника равны \(\displaystyle 5\) и \(\displaystyle 10\), а угол между ними равен \(\displaystyle 60^{\circ}.\) Через центр вписанной окружности этого треугольника и концы третьей стороны проведена окружность. Найдите ее радиус.
| 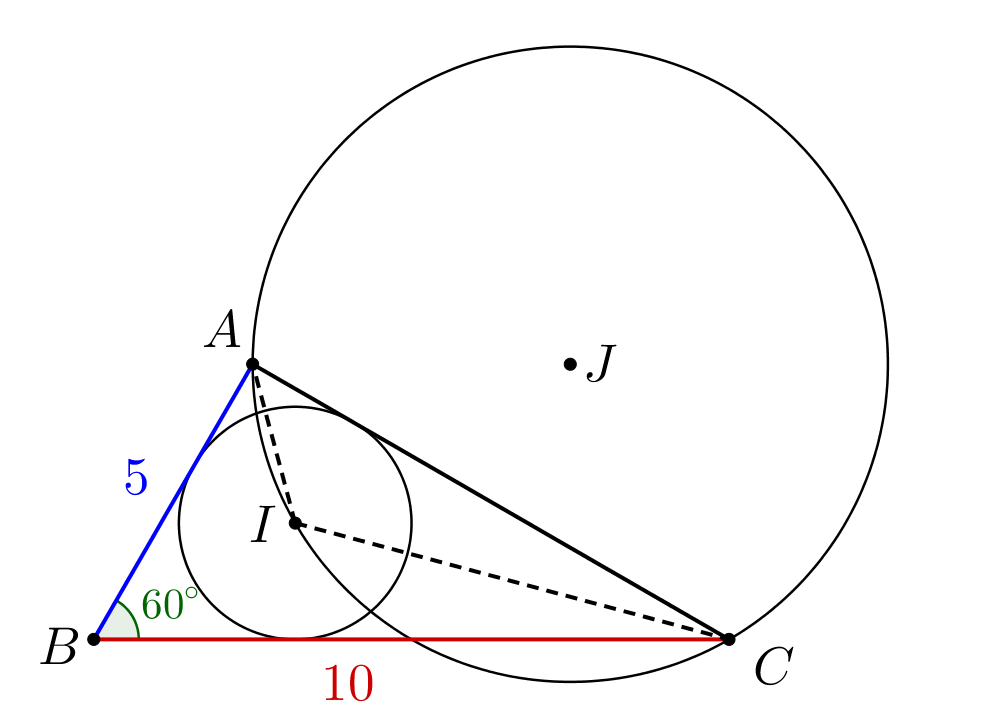 |
Радиус окружности, описанной около треугольника \(\displaystyle AIC\small,\) можно вычислить по теореме синусов:
\(\displaystyle 2R=\frac{AC}{\sin\angle AIC}\small.\)
Тогда найдем угол \(\displaystyle AIC\) и сторону \(\displaystyle AC\small.\)
\(\displaystyle AC=5\sqrt3\small.\)
По теореме косинусов для треугольника \(\displaystyle ABC\small{:}\) \(\displaystyle AC^2=AB^2+BC^2-2AB\cdot BC\cdot \cos\angle ABC\small.\) Подставим в формулу известные значения и вычислим длину \(\displaystyle AC\small{:}\) \(\displaystyle AC^2=5^2+10^2-2\cdot5\cdot 10\cdot \cos60^\circ=75\small.\) \(\displaystyle AC=\sqrt{75}=5\sqrt3\small.\) | 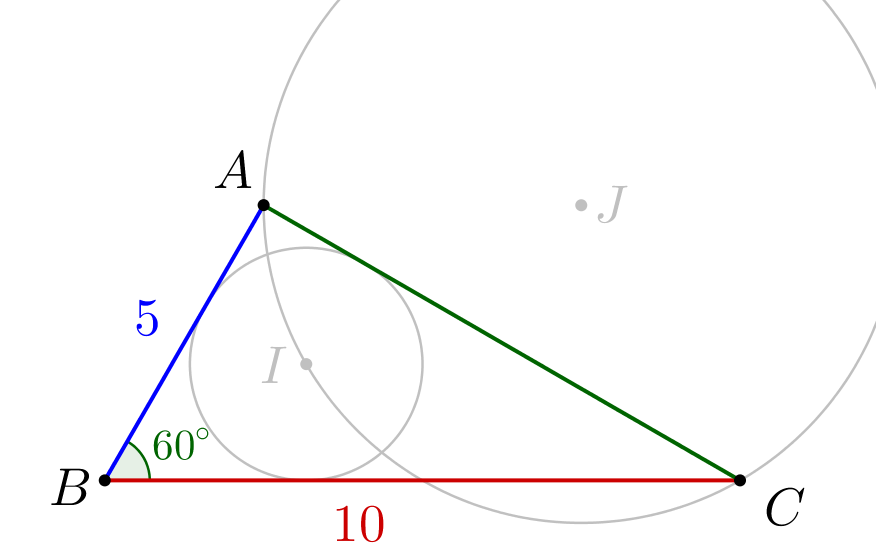 |
\(\displaystyle \angle AIC=120^\circ\small.\)
\(\displaystyle \angle AIC=180^\circ-(\angle CAI+\angle ACI)\small.\) Точка \(\displaystyle I\) – центр вписанной окружности треугольника \(\displaystyle ABC\small.\) То есть точка \(\displaystyle I\) – точка пересечения биссектрис углов треугольника \(\displaystyle ABC\small.\) Тогда: \(\displaystyle \angle CAI=\angle BAC:2\small,\) \(\displaystyle \angle ACI=\angle ACB:2\small.\) \(\displaystyle \begin{aligned} \angle CAI+\angle ACI=(\angle BAC+\angle ACB):2= \\[5px] =(180^\circ-\angle ABC):2=120^\circ:2=60^\circ\small.\end{aligned}\) Тогда \(\displaystyle \angle AIC=180^\circ-60^\circ=120^\circ\small.\) | 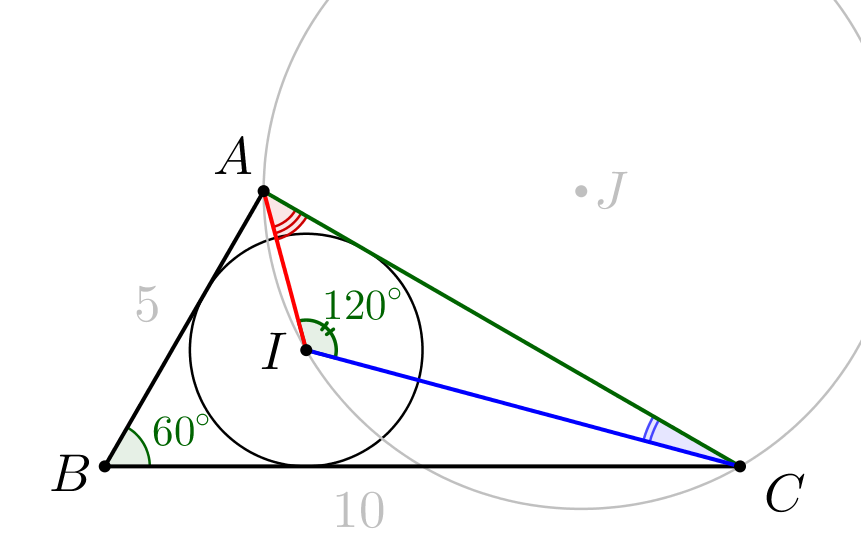 |
Получаем
\(\displaystyle \begin{aligned}2R&=\frac{AC}{\sin\angle AIC}=\frac{5\sqrt3}{\sin120^\circ}\small,\\[10px]R&=\frac{5\sqrt3}{2}:\frac{\sqrt3}{2}\small,\\[10px]R&=5\small.\end{aligned}\)
Ответ: \(\displaystyle 5\small.\)