В треугольнике \(\displaystyle ABC\) провели отрезок \(\displaystyle BK\small,\) который делит угол \(\displaystyle B\) на углы \(\displaystyle \alpha\) и \(\displaystyle \beta\small.\) Сторона \(\displaystyle AB=a\small,\) сторона \(\displaystyle BC=b\small,\) а угол \(\displaystyle AKB=\gamma\small.\)
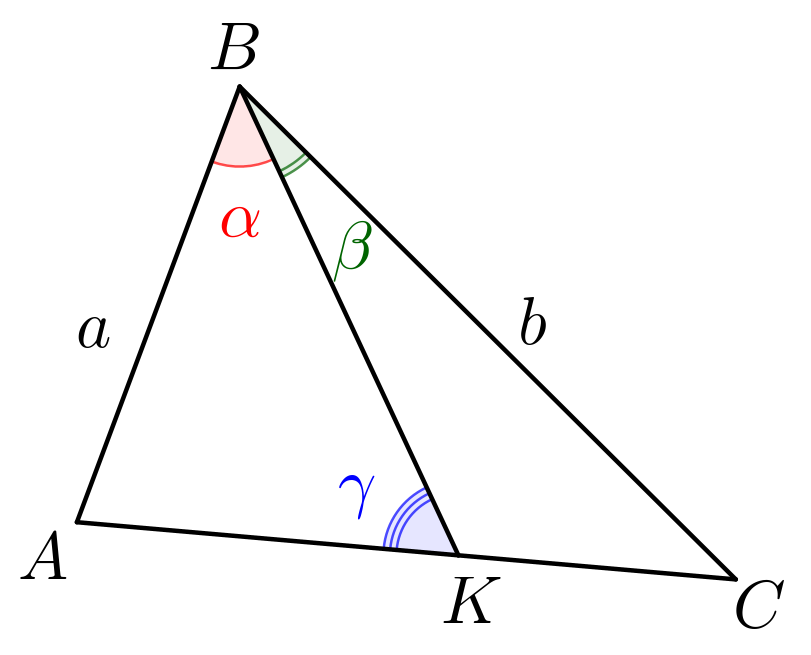
Используя теорему синусов, выразите сторону \(\displaystyle AC\) через \(\displaystyle \sin\alpha,\,\sin\beta,\,\sin\gamma\) и \(\displaystyle a,\,b{\small.}\)
(Выберите верный ответ из списка.)
Теорема синусов
В треугольнике отношения сторон к синусам противолежащих углов одинаковы и равны удвоенному радиусу описанной окружности: \(\displaystyle \frac{\color{Purple}{a}}{\sin\color{Purple}{\alpha}}=\frac{\color{green}{b}}{\sin\color{green}{\beta}}=\frac{\color{blue}{c}}{\sin\color{blue}{\gamma}}=2\color{red}{R}{\small.}\) | 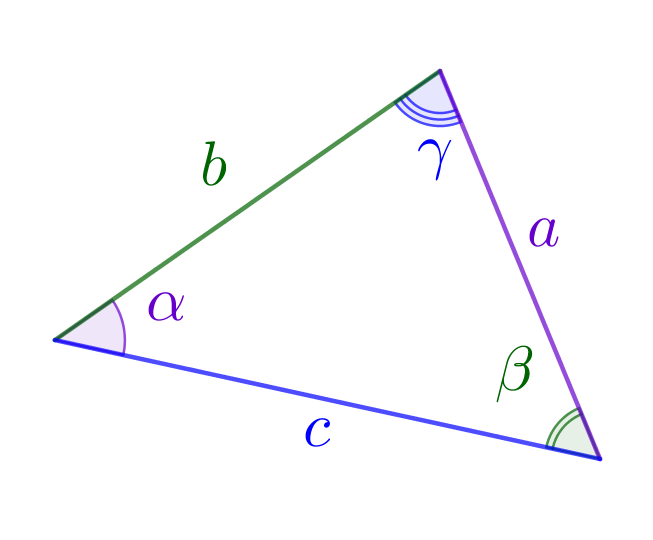 |
Отрезок \(\displaystyle AC\) состоит из отрезков \(\displaystyle AK\) и \(\displaystyle KC\small.\) Поэтому, чтобы выразить \(\displaystyle AC\) через известные величины, выразим \(\displaystyle AK\) и \(\displaystyle KC\small,\)а затем вычислим их сумму.
\(\displaystyle AK=\frac{a\sin\alpha}{\sin\gamma}\small.\)
Рассмотрим треугольник \(\displaystyle ABK\small.\) В этом треугольнике известны сторона \(\displaystyle \color{blue}a\) и два угла:\(\displaystyle \color{red}{\alpha}\) и \(\displaystyle \color{blue}\gamma\small.\) По теореме синусов: \(\displaystyle \frac{\color{blue}{a}}{\sin\color{blue}\gamma}=\frac{\color{red}{AK}}{\sin\color{red}\alpha}\small.\) | 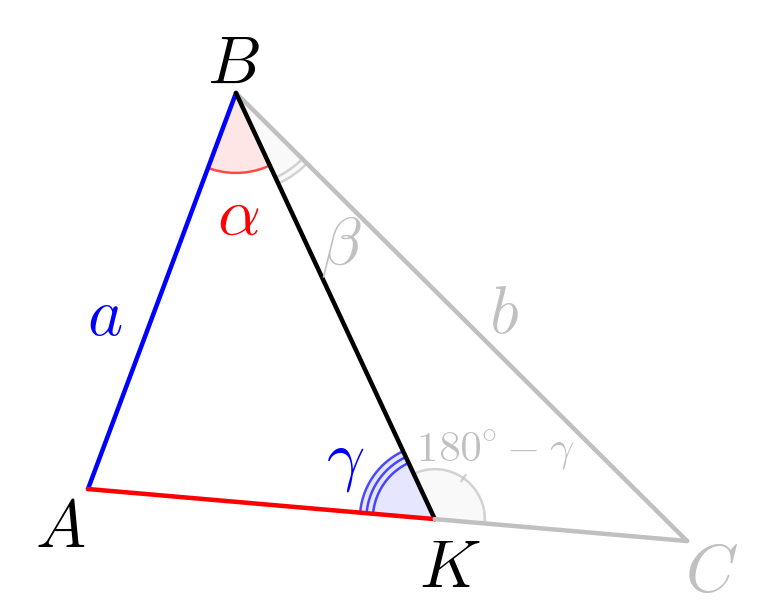 |
Выразим \(\displaystyle AK\small{:}\)
\(\displaystyle AK=\frac{a\sin\alpha}{\sin\gamma}\small.\)
\(\displaystyle KC=\frac{b\sin\beta}{\sin\gamma}\small.\)
Рассмотрим треугольник \(\displaystyle KBC\small.\) В этом треугольнике известны сторона \(\displaystyle \color{blue}b\) и угол \(\displaystyle \color{green}\beta\small.\) \(\displaystyle \angle BKC=180^\circ-\angle AKB=180^\circ-\color{blue}\gamma\small.\) По теореме синусов: \(\displaystyle \frac{\color{blue}{b}}{\sin(\color{blue}{180^\circ-\gamma})}=\frac{\color{green}{KC}}{\sin\color{green}\beta}\small.\) | 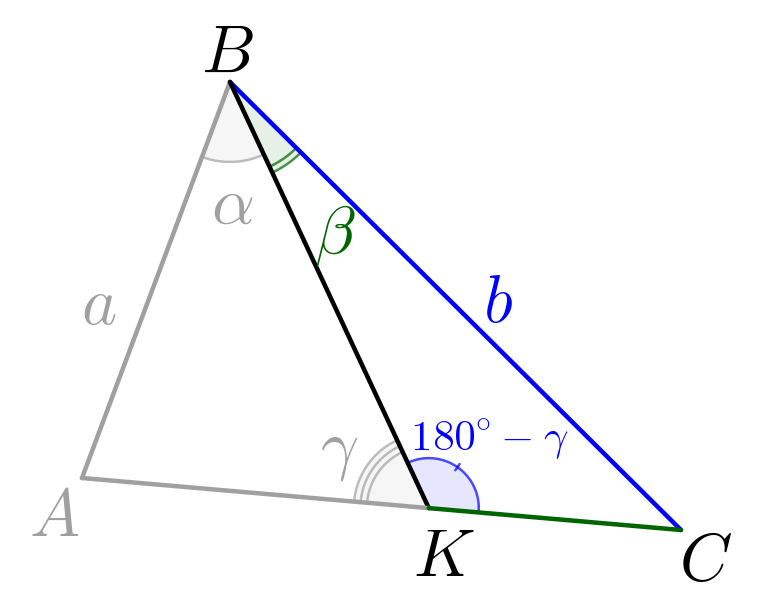 |
Выразим \(\displaystyle KC\small{:}\)
\(\displaystyle KC=\frac{b\sin\beta}{\sin(180^\circ-\gamma)}\small.\)
Учитывая, что \(\displaystyle \sin(180^\circ-\gamma)=\sin\gamma\small,\) выполним преобразования:
\(\displaystyle KC=\frac{b\sin\beta}{\sin\gamma}\small.\)
Вычислим сумму этих отрезков:
\(\displaystyle AC=AK+KC=\frac{a\sin\alpha}{\sin\gamma}+\frac{b\sin\beta}{\sin\gamma}=\frac{a\sin\alpha+b\sin\beta}{\sin\gamma}\small.\)
Ответ: \(\displaystyle AC=\frac{a\sin\alpha+b\sin\beta}{\sin\gamma}\small.\)