На рисунке треугольник \(\displaystyle ABC\) и ещё три треугольника. Отмечены равные элементы.
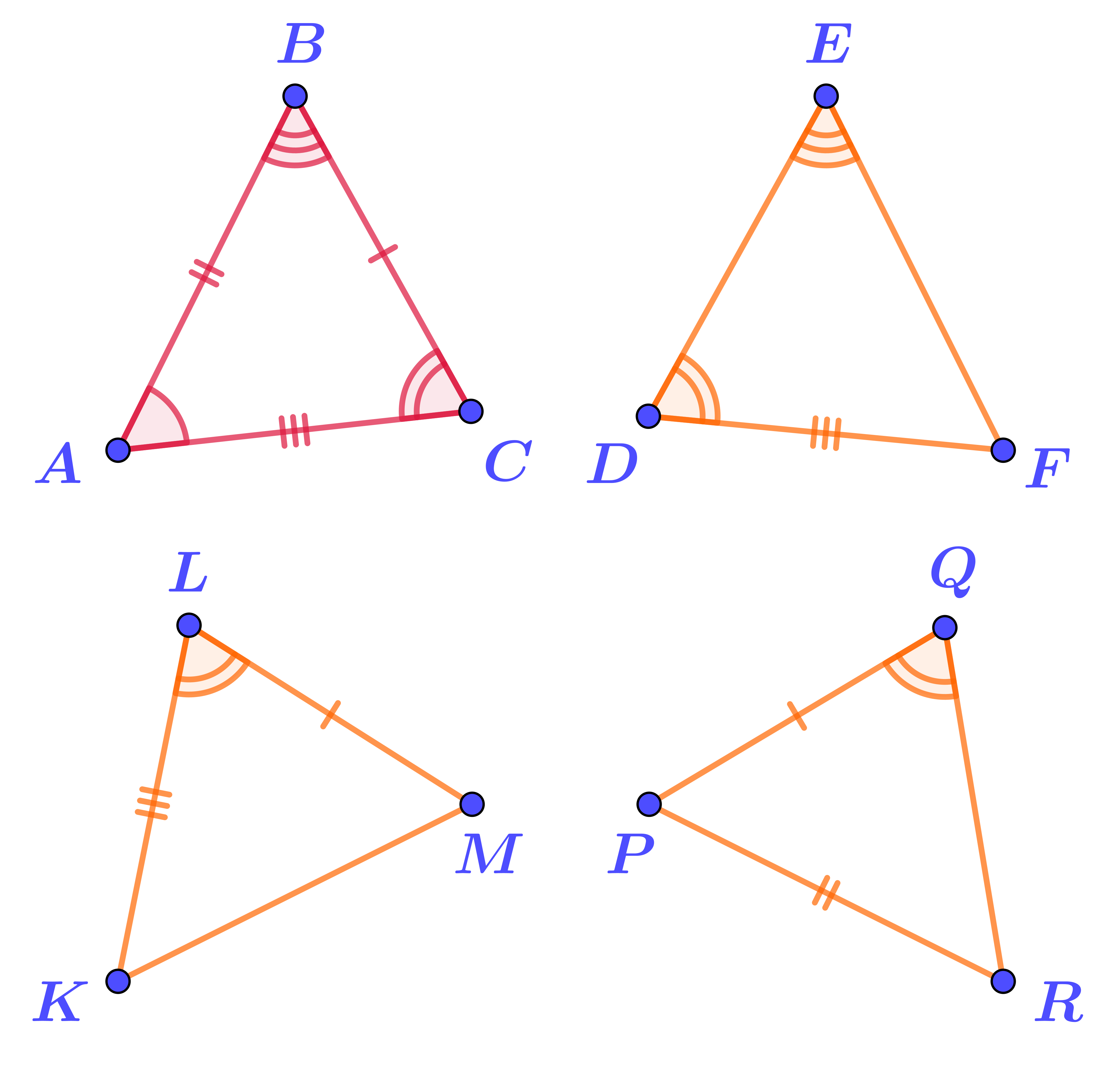
Пользуясь первым признаком равенства треугольников, можно доказать, что один из треугольников равен треугольнику \(\displaystyle ABC{\small .}\) Какой именно?
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
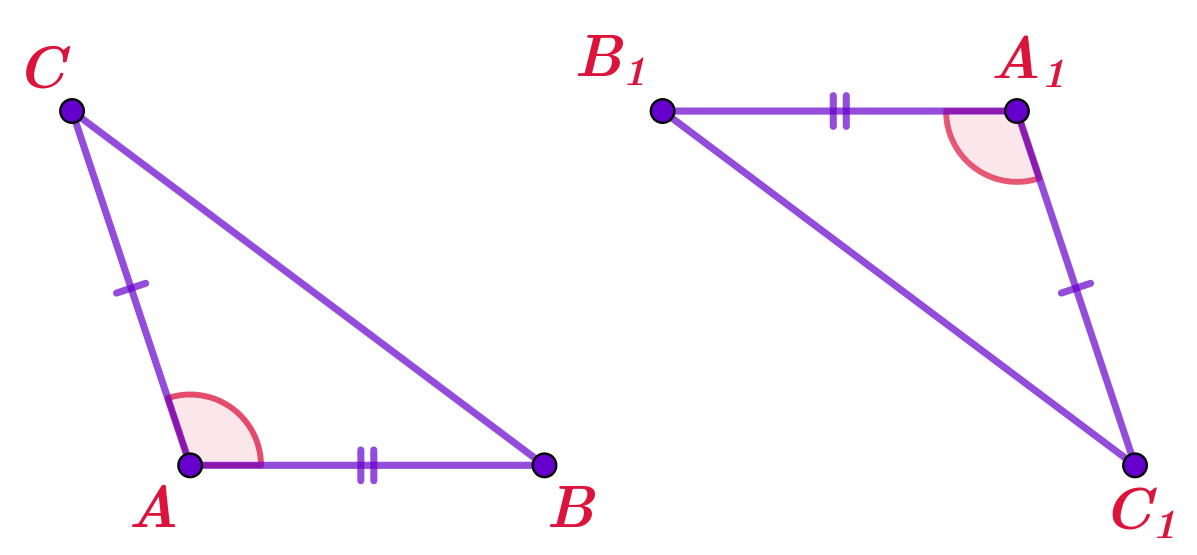
\(\displaystyle\left\{\begin{array}{}AB=A_1B_1\\AC=A_1C_1\\\angle BAC=\angle B_1A_1C_1\end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}ABC={\bf\triangle}A_1B_1C_1\right.\)
1. В треугольнике \(\displaystyle EDF\) не находим двух сторон, равных сторонам исходного треугольника.
Значит, применить первый признак равенства треугольников нельзя.
2. В треугольнике \(\displaystyle QPR\) про угол между сторонами \(\displaystyle PQ\) и \(\displaystyle PR\) неизвестно, равен ли он углу исходного треугольника.
Значит, применить первый признак равенства треугольников нельзя.
3. Треугольник \(\displaystyle KLM\) равен исходному треугольнику \(\displaystyle ABC\) по двум сторонам и углу между ними:
\(\displaystyle \left\{\begin{array}{ll}CA=LK\\CB=LM\\\angle BCA=\angle MLK\end{array}{\LARGE\Rightarrow} \quad {\bf\triangle}ABC={\bf\triangle}KLM\text{ \normalsize\it(по первому признаку)}\right.\)
Ответ: \(\displaystyle {\triangle}ABC={\triangle}KLM{\small .}\)