Многоугольник \(\displaystyle ABCDEFG\) составлен из многоугольников \(\displaystyle ABCG{\small,}\) \(\displaystyle CDG{\small,}\) \(\displaystyle DFG\) и \(\displaystyle DEF{\small,}\) площади которых равны \(\displaystyle 15{\small,}\) \(\displaystyle 10{\small,}\) \(\displaystyle 12\) и \(\displaystyle 6\) соответственно. Найдите площадь многоугольника \(\displaystyle ABCDEFG{\small.}\)
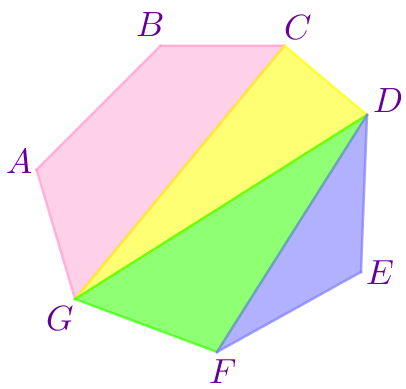
\(\displaystyle S_{ABCDEFG}=\)
Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
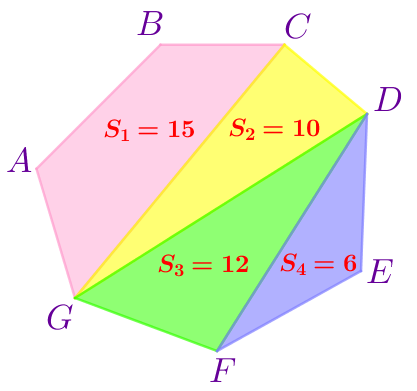 | Обозначим:
|
Многоугольник \(\displaystyle ABCDEFG\) составлен из многоугольников \(\displaystyle ABCG{\small,}\) \(\displaystyle CDG{\small,}\) \(\displaystyle DFG\) и \(\displaystyle DEF{\small,}\) следовательно,
\(\displaystyle S_{ABCDEFG}=S_1+S_2+S_3+S_4=15+10+12+6=43{\small.}\)
Ответ: \(\displaystyle S_{ABCDEFG}=43{\small.}\)