В прямоугольном треугольнике \(\displaystyle ABC\) с прямым углом \(\displaystyle C\) и высотой \(\displaystyle CH\) отмечены отрезки \(\displaystyle AC=a{\small,}\) \(\displaystyle AB=c{\small,}\) \(\displaystyle AH=a_{c}{\small.}\)
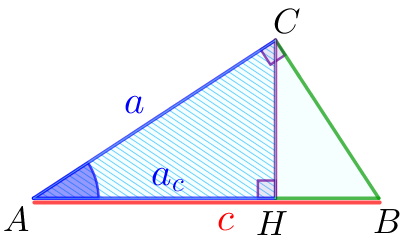
Используя то, что треугольники \(\displaystyle ABC\) и \(\displaystyle ACH\) подобны, выразите \(\displaystyle a\) через \(\displaystyle c\) и \(\displaystyle a_{c}\small.\)
Треугольники \(\displaystyle ABC\) и \(\displaystyle ACH\) подобны. Тогда их соответственные стороны пропорциональны:
\(\displaystyle \frac{AB}{AC}=\frac{AC}{AH}{\small.}\)
Или подставляя \(\displaystyle c,\,a,\,a_{c}{\small:}\)
\(\displaystyle \frac{c}{a}=\frac{a}{a_{c}}{\small.} \)
По свойству пропорции:
\(\displaystyle a^2=ca_{c}{\small;}\)
\(\displaystyle a=\sqrt{ca_{c}}{\small.}\)
Ответ: \(\displaystyle a=\sqrt{ca_{c}}{\small.}\)