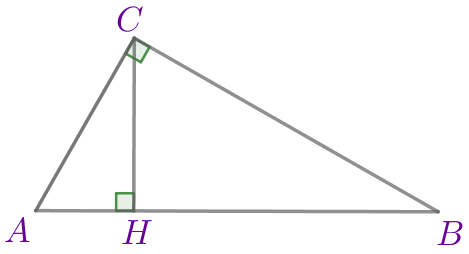
В прямоугольном треугольнике \(\displaystyle ABC\) с прямым углом \(\displaystyle C\) и высотой \(\displaystyle CH{\small:}\) \(\displaystyle AC=8{\small,}\) \(\displaystyle AB=16{\small.}\) Найдите длину отрезка \(\displaystyle AH{\small.}\)
\(\displaystyle AH=\)
\(\displaystyle ABC\) – прямоугольный треугольник:
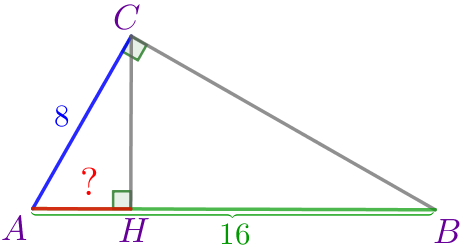 |
Требуется найти длину отрезка \(\displaystyle AH{\small.}\)
|
Воспользуемся правилом:
Катет прямоугольного треугольника есть среднее геометрическое для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
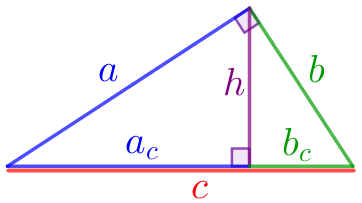 | \(\displaystyle \Large \color{blue}{a}=\sqrt{\color{red}{c}\cdot \color{blue}{a_{c}}}\\ \) \(\displaystyle \Large \color{green}{b}=\sqrt{\color{red}{c}\cdot \color{green}{b_{c}}}\) |
Значит,
\(\displaystyle AC=\sqrt{AB \cdot AH}{\small;}\)
\(\displaystyle AC^2=AB \cdot AH{\small.}\)
Подставим известные значения и найдем \(\displaystyle AH{\small:}\)
\(\displaystyle 8^2=16 \cdot AH{\small;}\)
\(\displaystyle AH=64:16=4{\small.}\)
Ответ: \(\displaystyle AH=4{\small.}\)