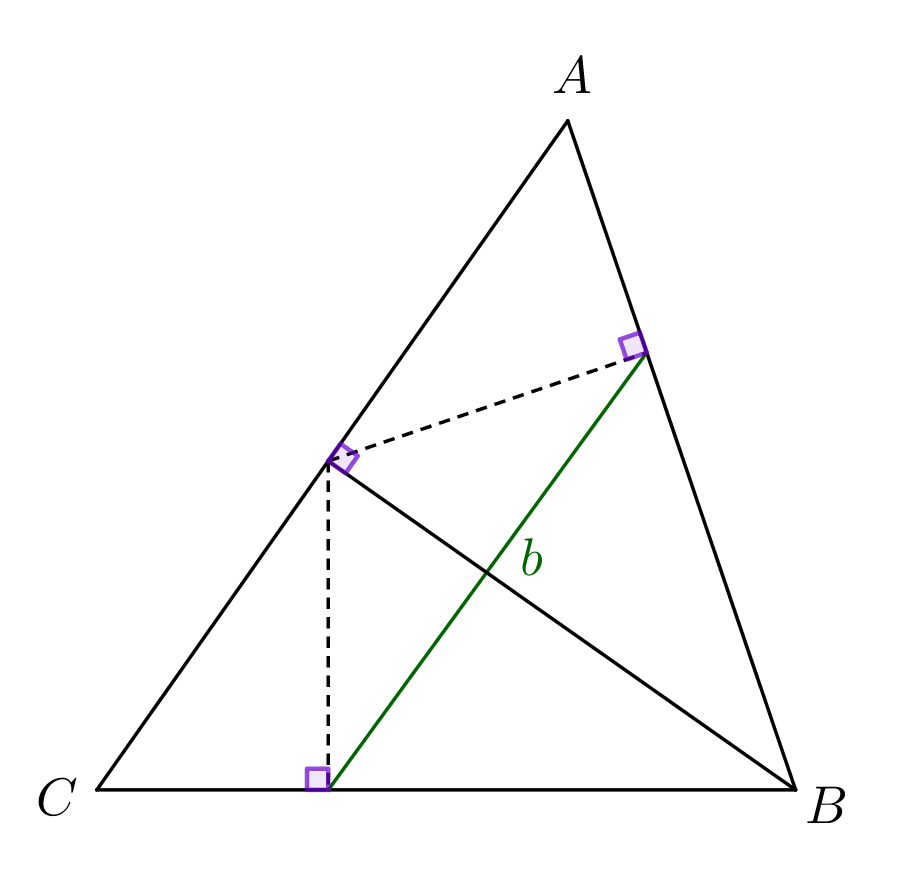
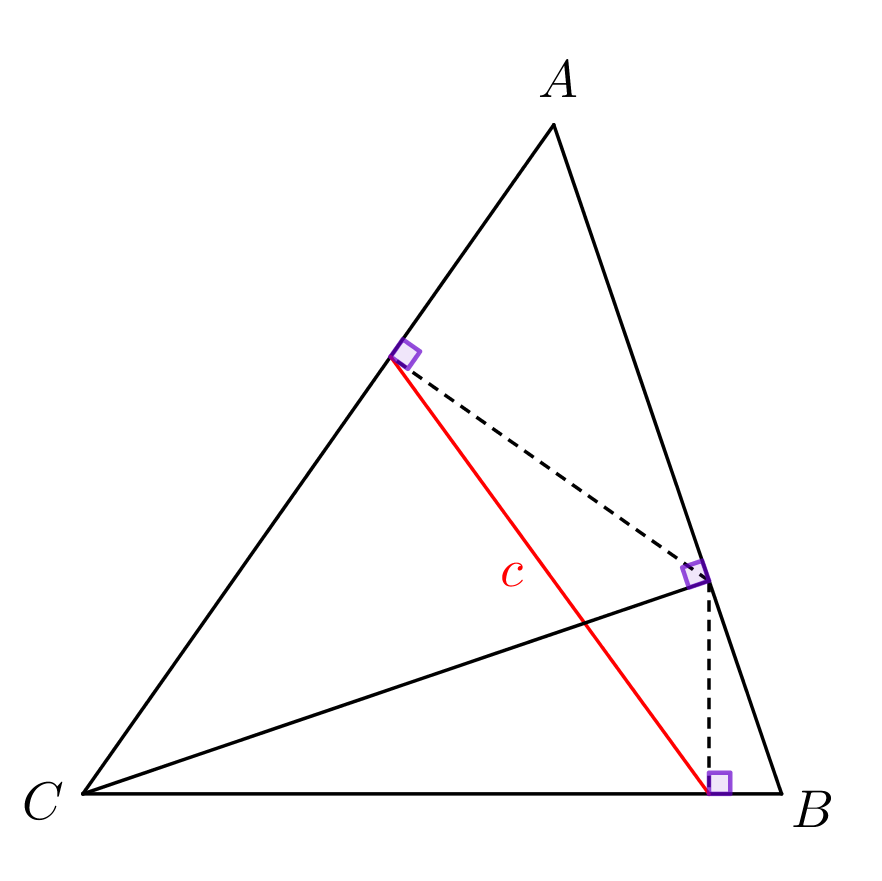
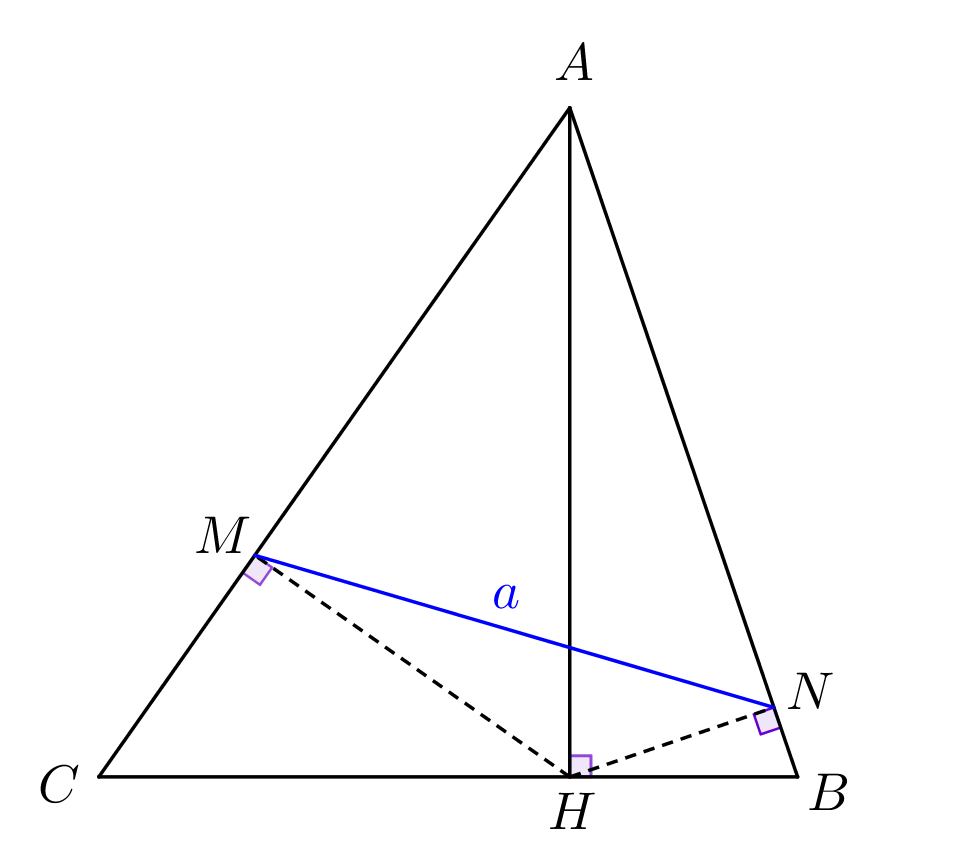
Основание высоты треугольника спроецировали на его стороны, соединили проекции, и получили отрезок \(\displaystyle a\small.\)
Стороны треугольника равны: \(\displaystyle AB=10,\,BC=11,\,AC=12\small.\) Найдите отношение отрезков:
Посмотрим на рисунок к задаче. Обозначим углы треугольника: \(\displaystyle \angle BAC=\alpha\small,\) \(\displaystyle \angle ABC=\beta\) и \(\displaystyle \angle ACB=\gamma\small.\) А еще обозначим длину высоты \(\displaystyle AH\) за \(\displaystyle h_a\small.\) | 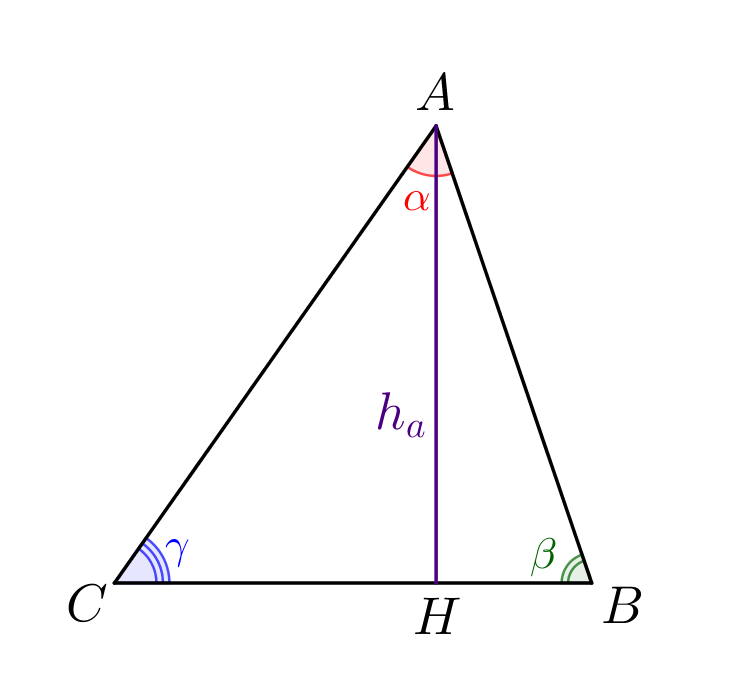 |
\(\displaystyle a=h_a\sin\alpha\small.\)
Посмотрим на прямоугольный треугольник \(\displaystyle ANH\small.\) Обозначим угол \(\displaystyle AHN\) за \(\displaystyle \varphi\small.\) Тогда в прямоугольном треугольнике \(\displaystyle ANH{:}\)
Тогда противолежащий катет: \(\displaystyle AN=AH\sin\angle H=h_a\sin\varphi\small.\) | 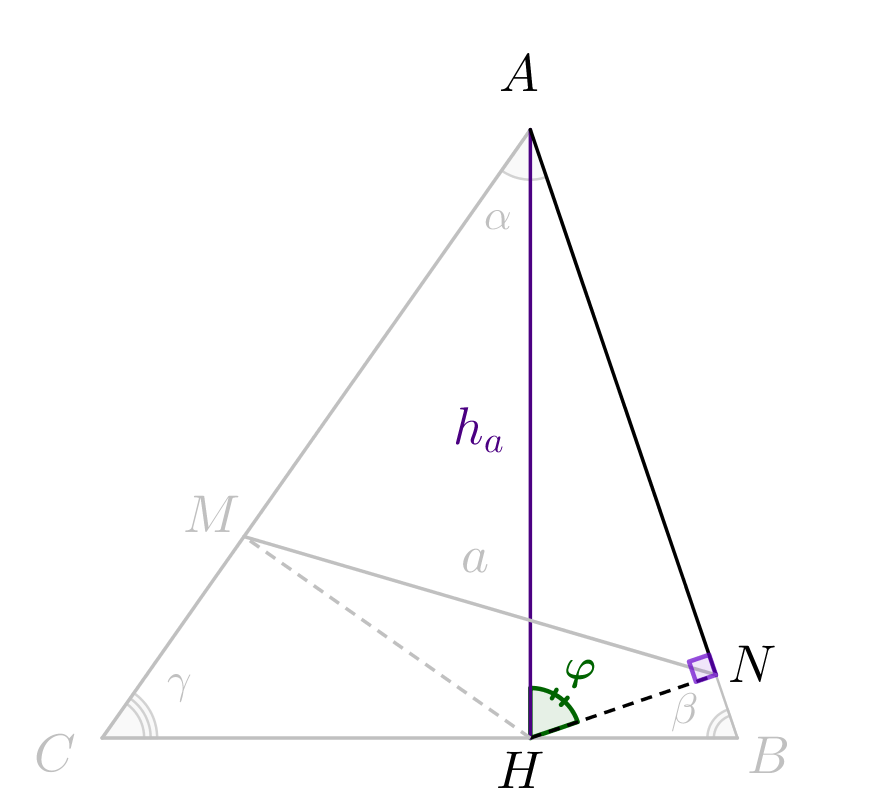 |
Отметим, что в четырехугольнике \(\displaystyle MANH\) сумма противоположных углов \(\displaystyle M\) и \(\displaystyle N\) равна \(\displaystyle 180^{\circ}\small.\) Значит, \(\displaystyle MANH\) – вписанный и углы, опирающиеся на одну дугу, равны.
\(\displaystyle \angle AMN=\angle AHN=\varphi.\)
Теперь, чтобы найти \(\displaystyle MN=a{ \small ,}\) воспользуемся теоремой синусов для треугольника \(\displaystyle MAN{\small:}\) \(\displaystyle \frac{MN}{\sin\alpha}=\frac{AN}{\sin\varphi}\small.\) Откуда получаем \(\displaystyle MN{\small:}\) \(\displaystyle MN=\frac{AN}{\sin\varphi}\cdot\sin\alpha=\frac{h_a\sin\varphi}{\sin\varphi}\cdot\sin\alpha=h_a\sin\alpha\small.\) То есть \(\displaystyle a=h_a\sin\alpha\small.\) | 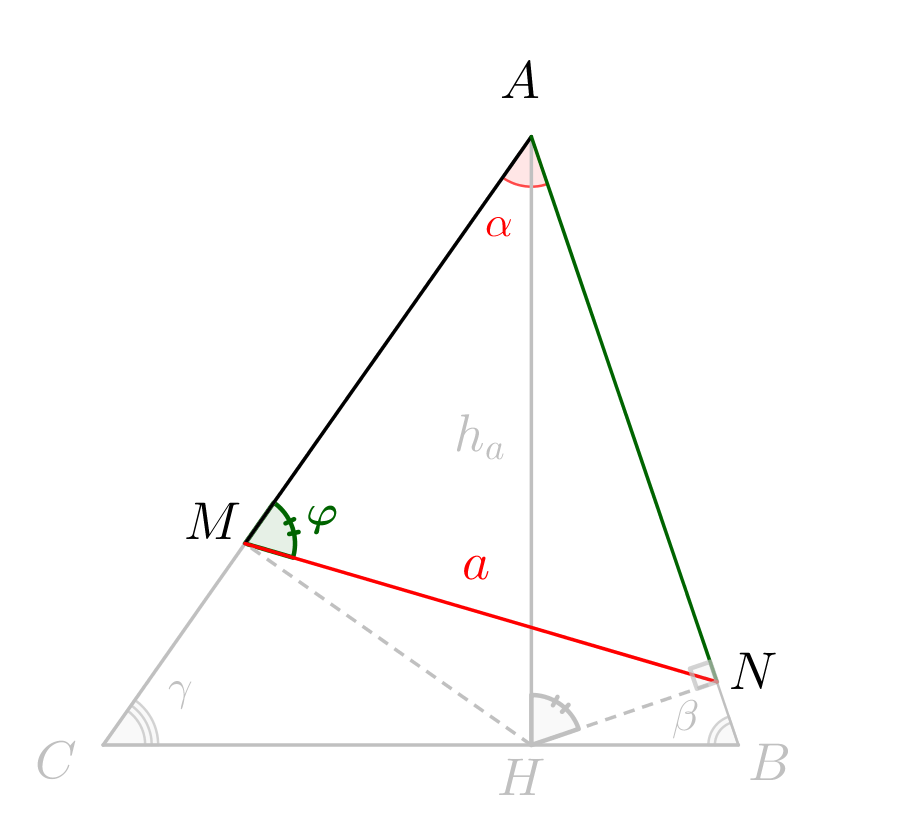 |
Аналогично для отрезков \(\displaystyle b\) и \(\displaystyle c\) получаем:
\(\displaystyle b=h_b\sin\beta\) и \(\displaystyle c=h_с\sin\gamma\)
\(\displaystyle a:b=1\small.\)
Посмотрим отношение двух отрезков:
\(\displaystyle \frac{a}{b}=\frac{h_a\sin\alpha}{h_b\sin\beta}\small.\)
В прямоугольном треугольнике \(\displaystyle AHB\) гипотенуза \(\displaystyle AB\) равна \(\displaystyle AB=\frac{h_a}{\sin\beta}\small.\) | 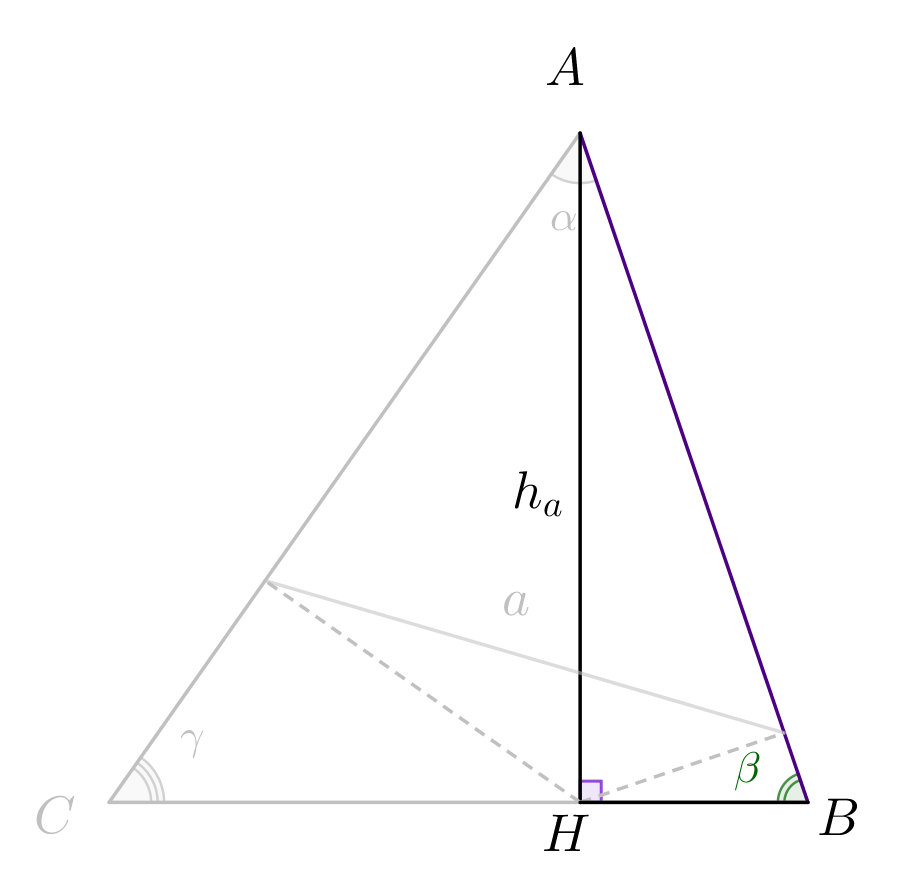 |
А в прямоугольном треугольнике \(\displaystyle ABK\) гипотенуза \(\displaystyle AB\) равна \(\displaystyle AB=\frac{h_b}{\sin\alpha}\small.\) | 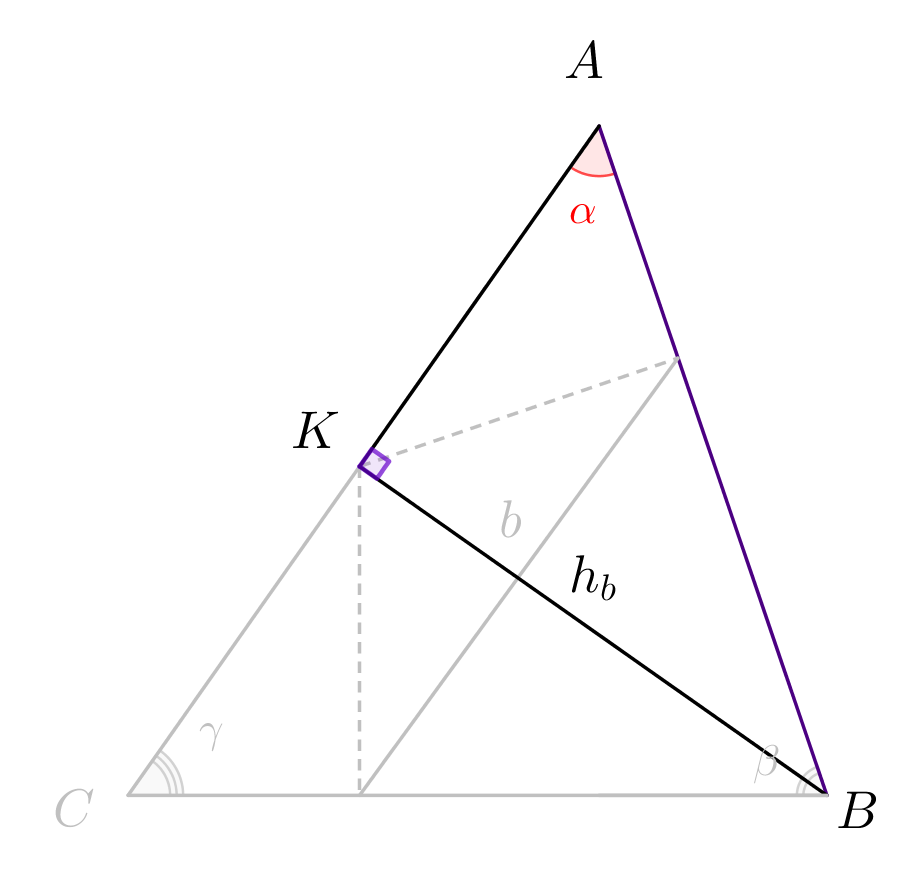 |
То есть
\(\displaystyle AB=\frac{h_a}{\sin\beta}=\frac{h_b}{\sin\alpha}\) и \(\displaystyle \frac{a}{b}=\frac{h_a\sin\alpha}{h_b\sin\beta}=\frac{AB}{AB}=1\small.\)
Аналогично \(\displaystyle a:c=1\) и тогда
\(\displaystyle a:b:c=1:1:1\small.\)
Ответ: \(\displaystyle a:b:c=1:1:1\small.\)