Задание
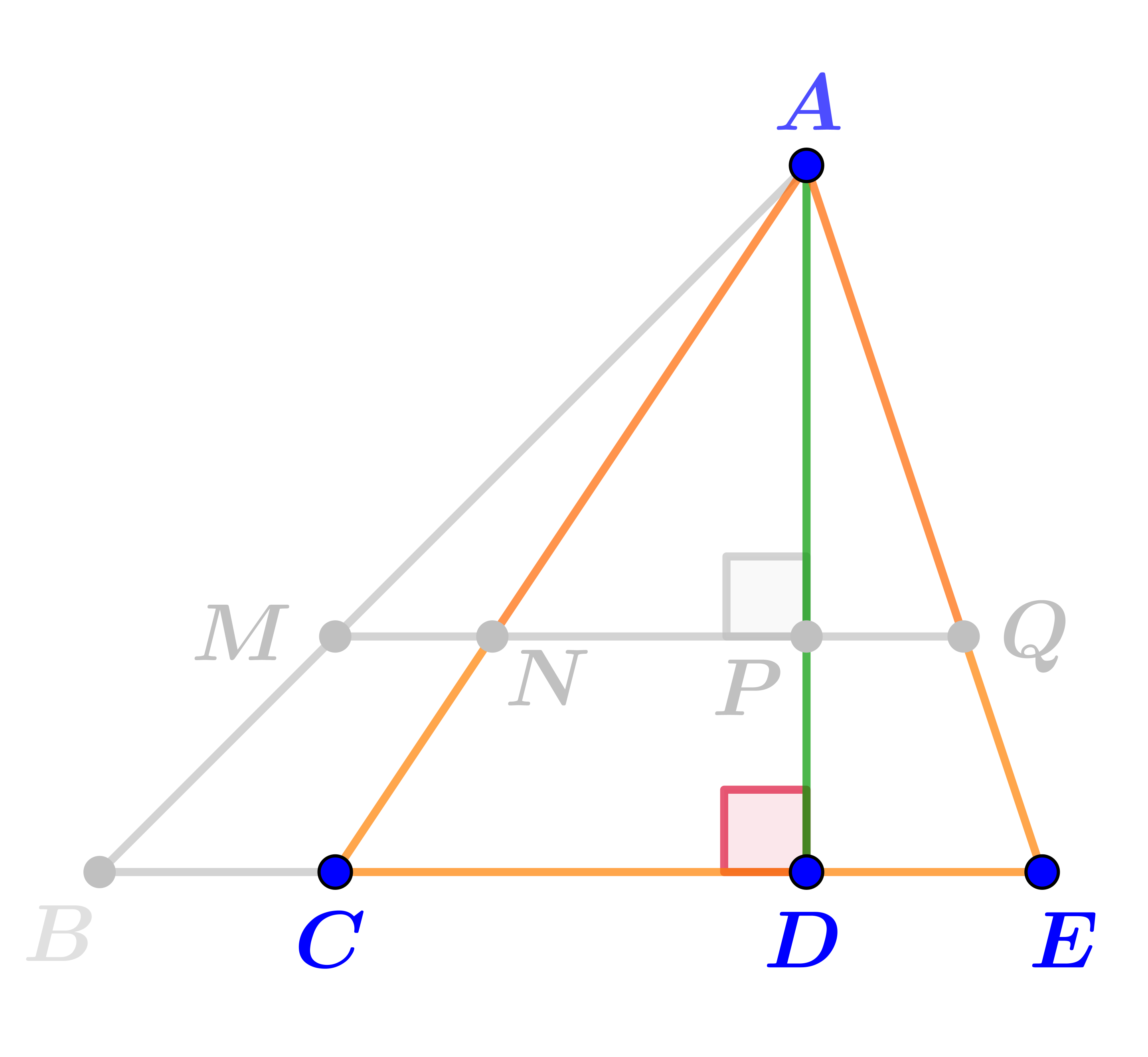
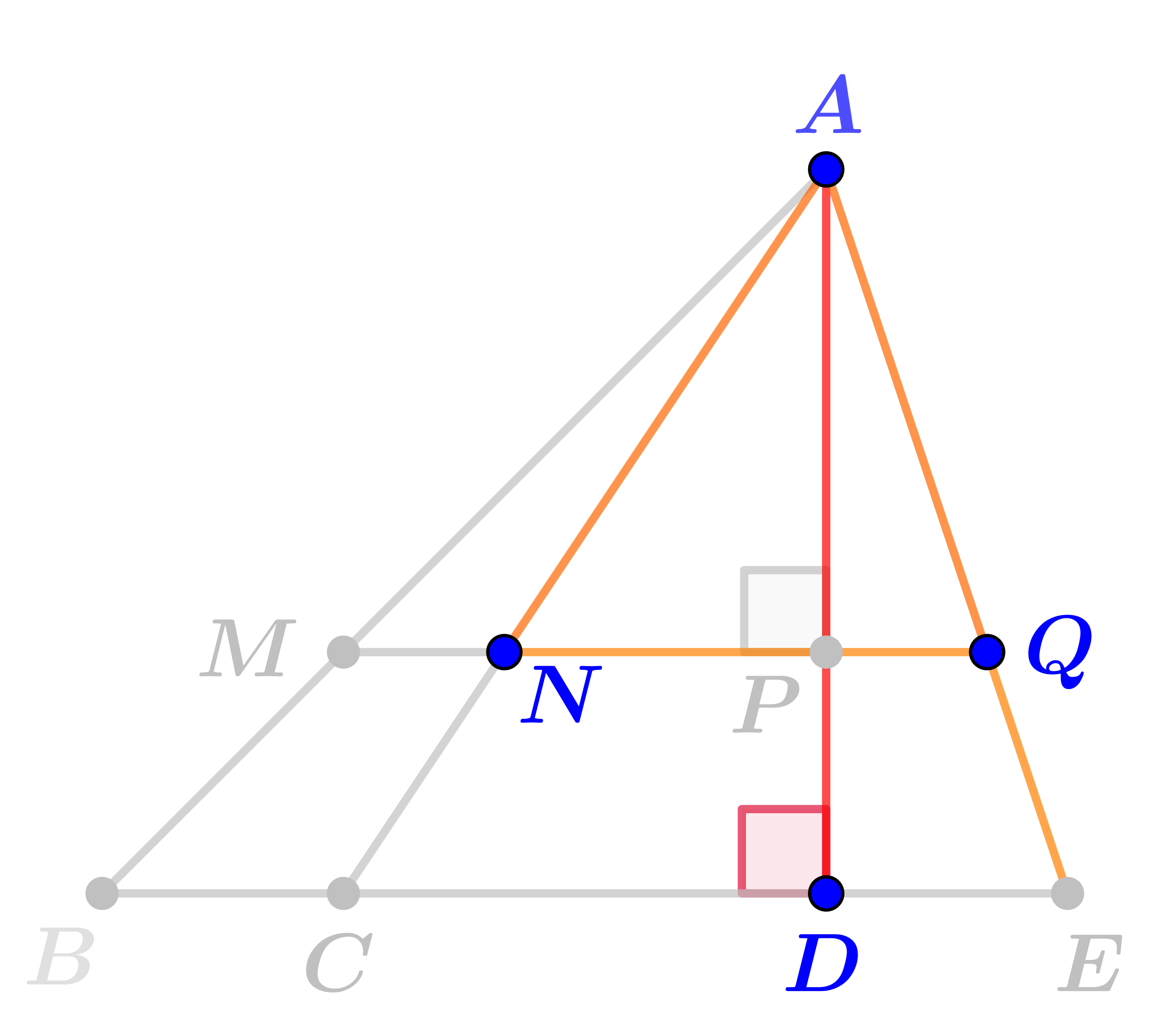
Прямые \(\displaystyle MQ\) и \(\displaystyle BE\) пересекают несколько лучей с вершиной в точке \(\displaystyle A{\small .}\)
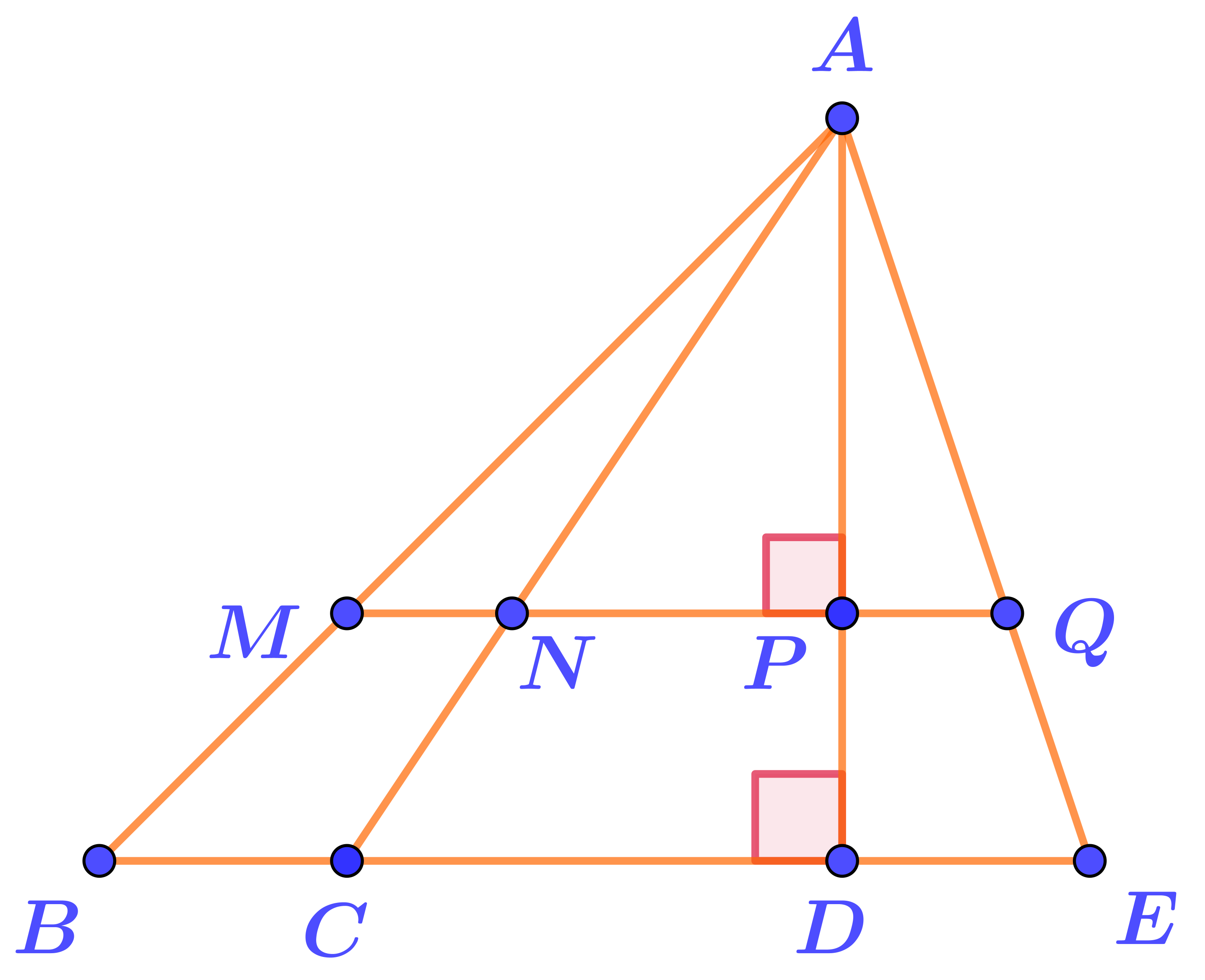
По данным рисунка выберите треугольники, высотой которых является отрезок \(\displaystyle AD{\small .}\)
Решение
Выберем треугольники, высотой которых является отрезок \(\displaystyle AD{\small .}\)
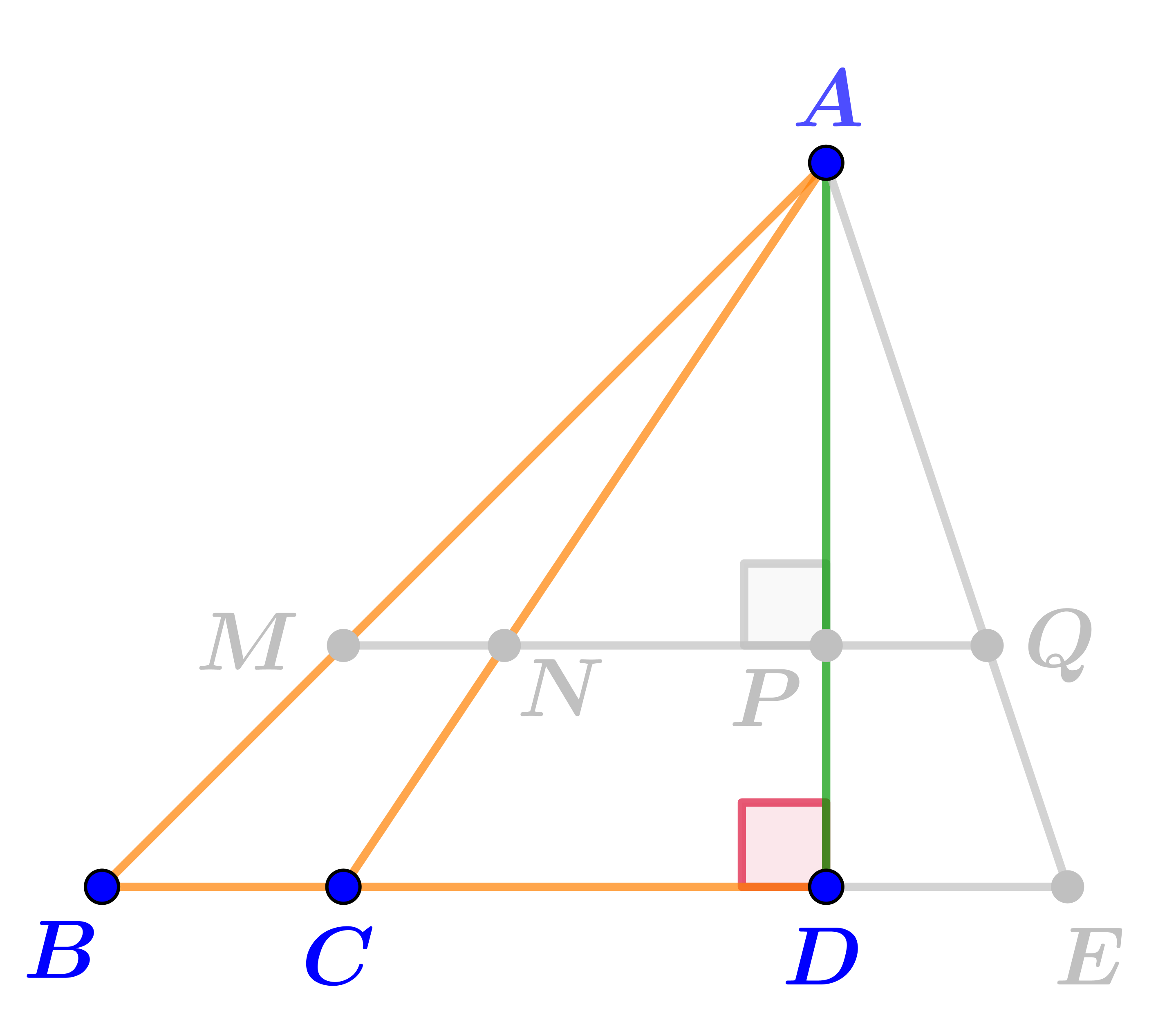
Отрезок \(\displaystyle AD\)\(\displaystyle \color{green}{\bf\small {является}}\)высотой треугольника\(\displaystyle ACE{\small .}\)
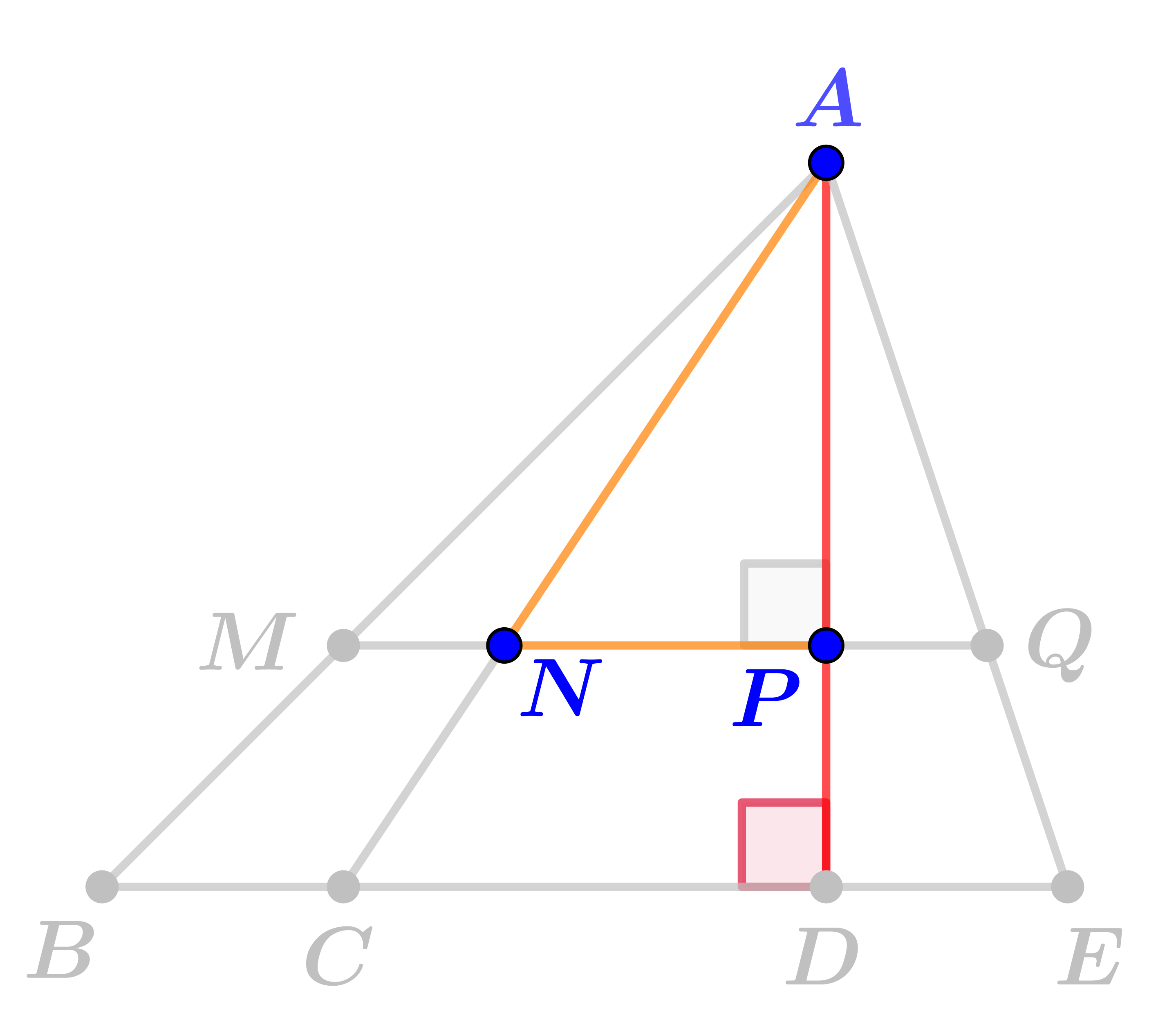
Отрезок \(\displaystyle AD\) \(\displaystyle \color{red}{\bf\small {не\;\;является}}\) высотой треугольника \(\displaystyle ANQ{\small .}\)
Отрезок \(\displaystyle AD\)\(\displaystyle \color{green}{\bf\small {является}}\)высотой треугольника\(\displaystyle ABC{\small .}\)
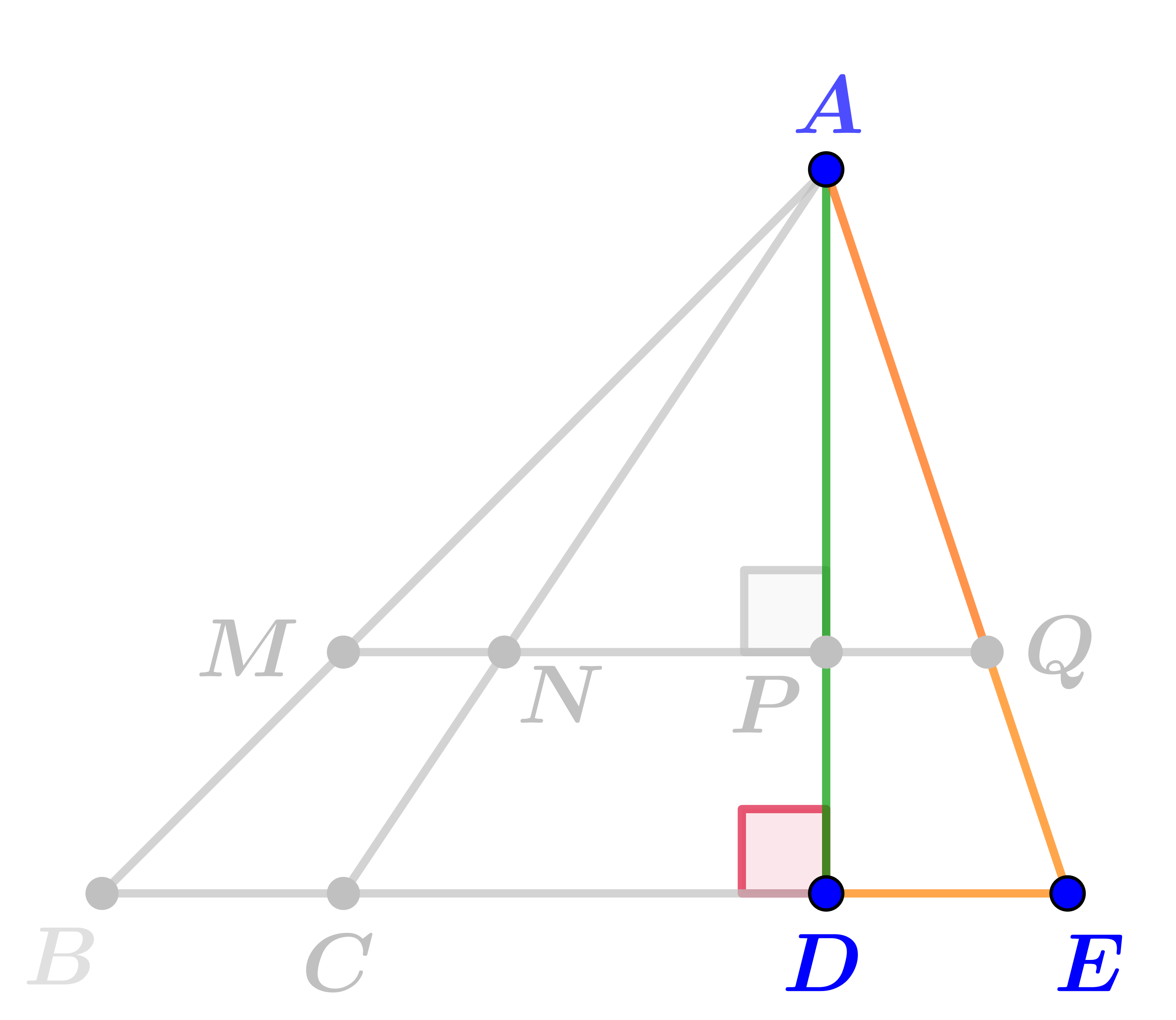
Отрезок \(\displaystyle AD\)\(\displaystyle \color{green}{\bf\small {является}}\)высотой треугольника\(\displaystyle ADE{\small .}\)
Отрезок \(\displaystyle AD\) \(\displaystyle \color{red}{\bf\small {не\;\;является}}\) высотой треугольника \(\displaystyle ANP{\small .}\)
Ответ: \(\displaystyle {\bf\triangle}ACE{\small ,}\) \(\displaystyle {\bf\triangle}ABC{\small ,}\) \(\displaystyle {\bf\triangle}ADE{\small .}\)