Задание
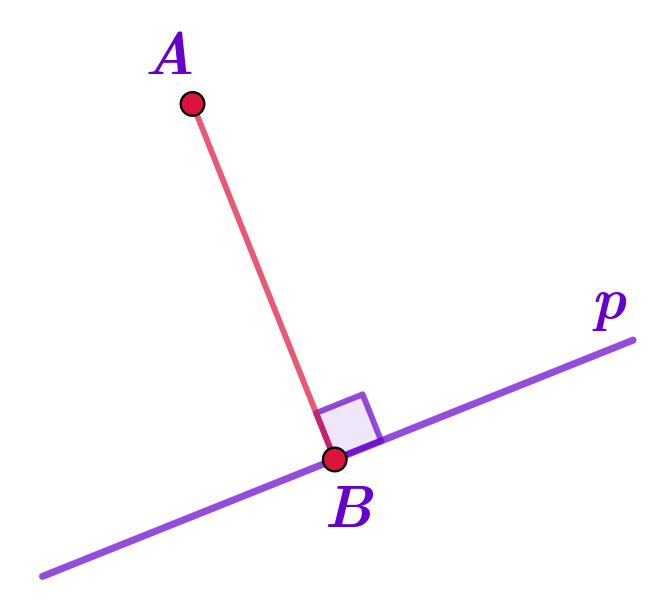
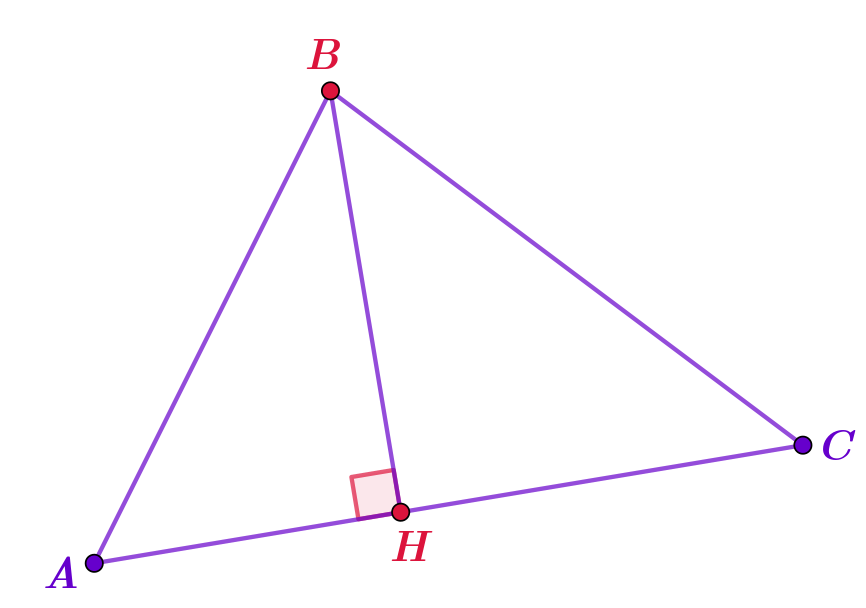
На клетчатой бумаге с длиной стороны клетки в \(\displaystyle 1\)см изображён треугольник \(\displaystyle ABC{\small .}\)
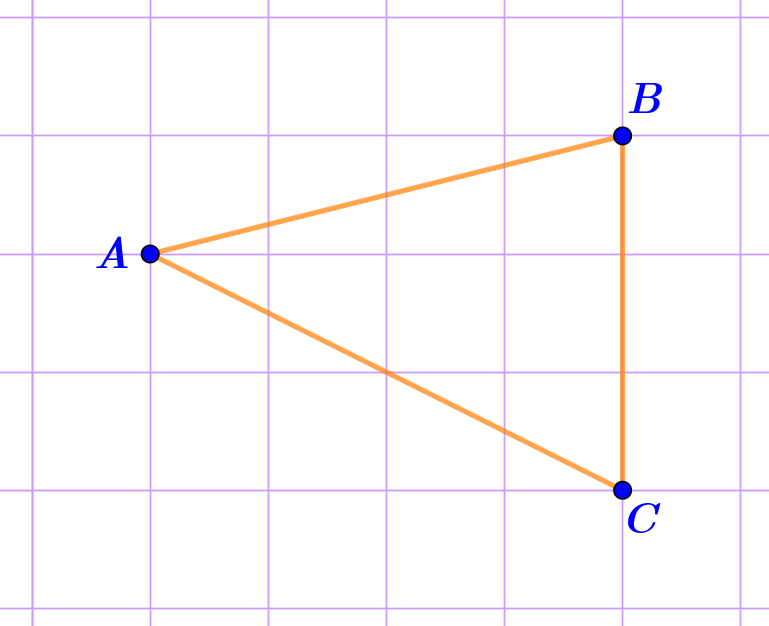
Какова длина его высоты \(\displaystyle AH\), проведённой к стороне \(\displaystyle BC{\small ?}\)
\(\displaystyle AH=\)см
Решение
1. Опустим из точки \(\displaystyle A\) перпендикуляр к прямой, содержащей сторону \(\displaystyle BC.\)
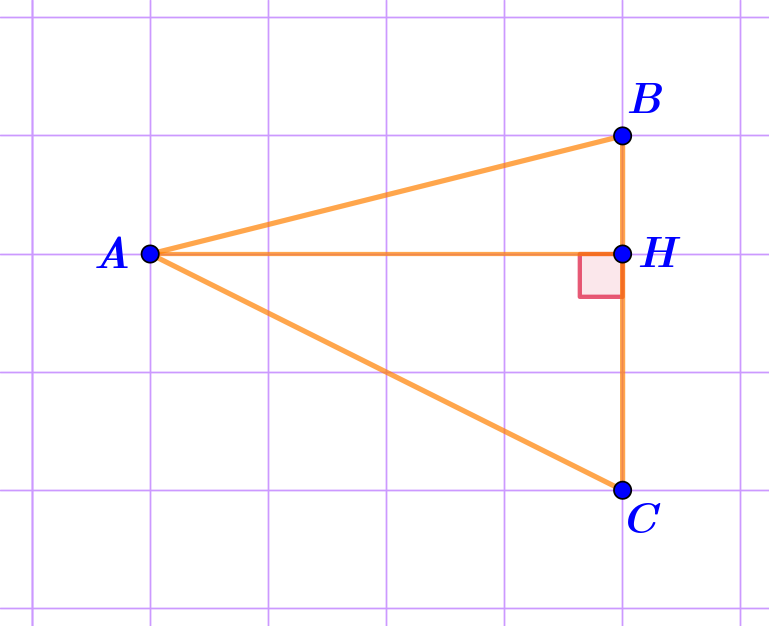
Получим отрезок \(\displaystyle AH{\small ,}\) причем
\(\displaystyle AH \perp BC{\small .}\)
2. Отрезок \(\displaystyle AH\)– высота треугольника \(\displaystyle ABC{\small .}\)
По рисунку, длина отрезка \(\displaystyle AH\) составляет \(\displaystyle 4\) клетки.
Длина стороны одной клетки по условию равна одному сантиметру.
Значит, длина высоты \(\displaystyle AH\) равна
\(\displaystyle 4 \cdot1 = 4\,{\footnotesize см} {\small .}\)
Ответ: \(\displaystyle 4\,{\footnotesize см} {\small .}\)