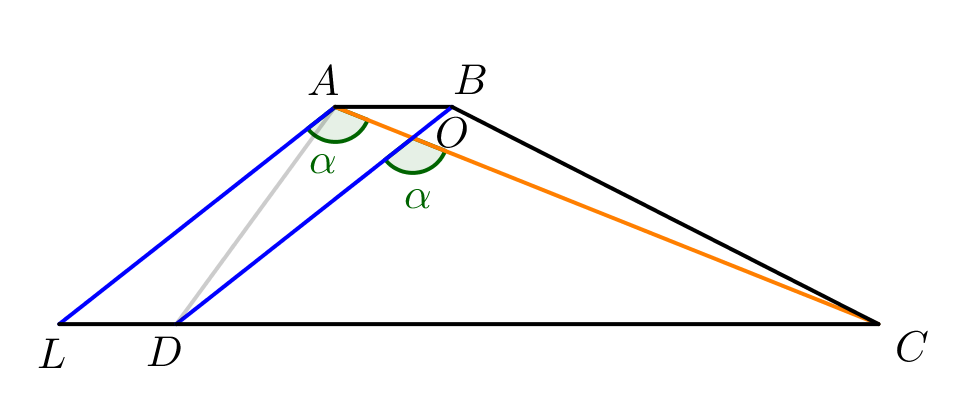
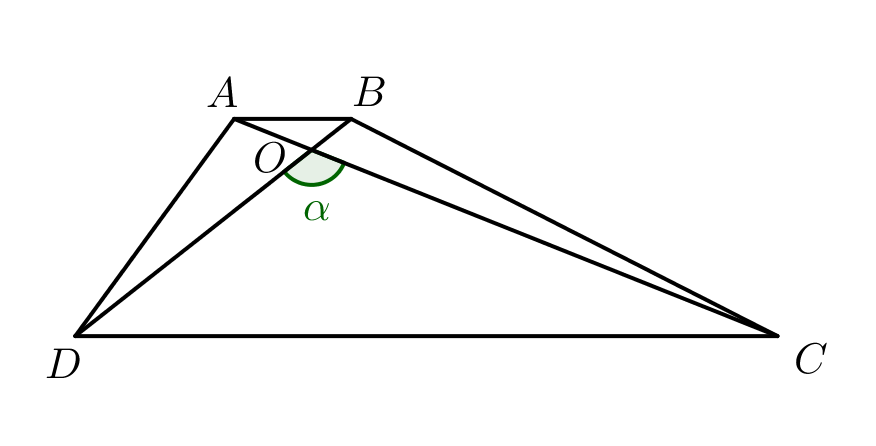
Основания трапеции равны \(\displaystyle 1\) и \(\displaystyle 6\small,\) а диагонали этой трапеции равны \(\displaystyle 3\) и \(\displaystyle 5\small.\) Найдите, под каким углом пересекаются диагонали.
(В ответе укажите острый угол.)
Обозначим за \(\displaystyle \alpha\) угол \(\displaystyle COD\small.\)
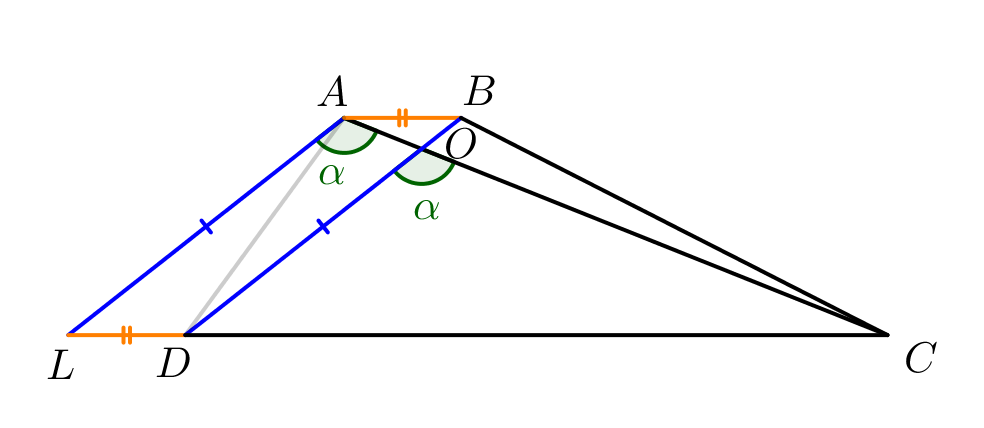
Попробуем сделать так, чтобы известные диагонали, \(\displaystyle \alpha\) и одно из оснований оказались в одном треугольнике. Для этого проведем через \(\displaystyle A\) прямую, параллельную \(\displaystyle BD\small.\) Обозначим за \(\displaystyle L\) точку пересечения этой прямой с прямой \(\displaystyle DC\small.\) | 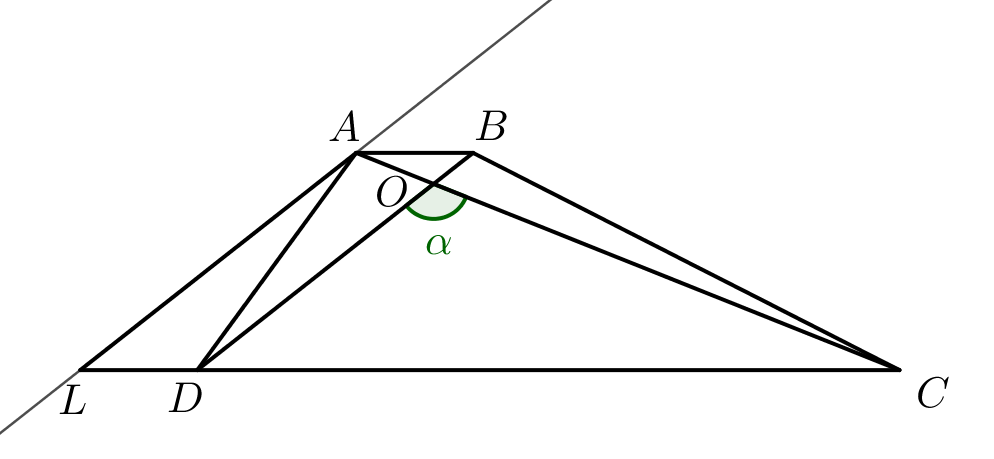 |
Тогда:
Получаем, что три стороны треугольника \(\displaystyle LAC:\) \(\displaystyle LA=3,\,AC=5\) и \(\displaystyle LC=LD+DC=1+6=7\small.\) | 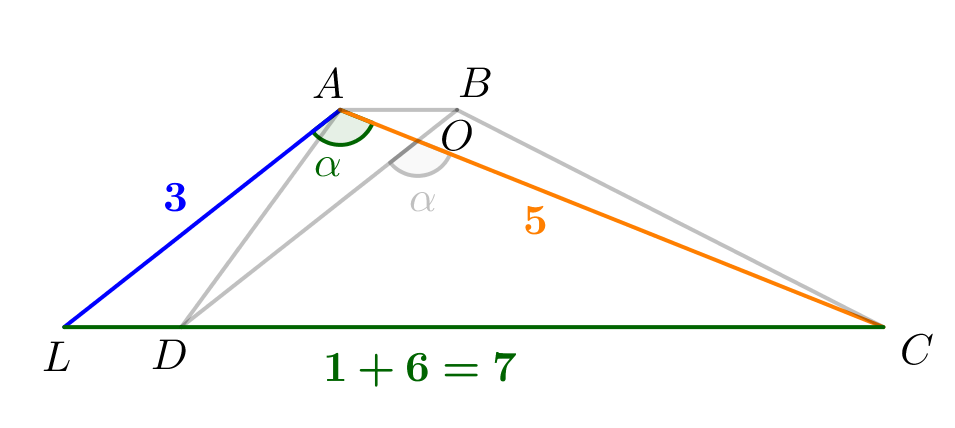 |
\(\displaystyle 7^2=3^2+5^2-2\cdot3\cdot5\cdot\cos\alpha\small,\)
\(\displaystyle \cos\alpha=-\frac{1}{2}\small.\)
\(\displaystyle \cos120^{\circ}=-\frac{1}{2}\small.\)
Угол \(\displaystyle 120^{\circ}\) – тупой. А второй угол между диагоналями дополняет его до \(\displaystyle 180^{\circ}\small.\) То есть равен \(\displaystyle 180^{\circ}-120^{\circ}=60^{\circ}\small.\) Значит, острый угол между диагоналями равен \(\displaystyle 60^{\circ}\small.\) | 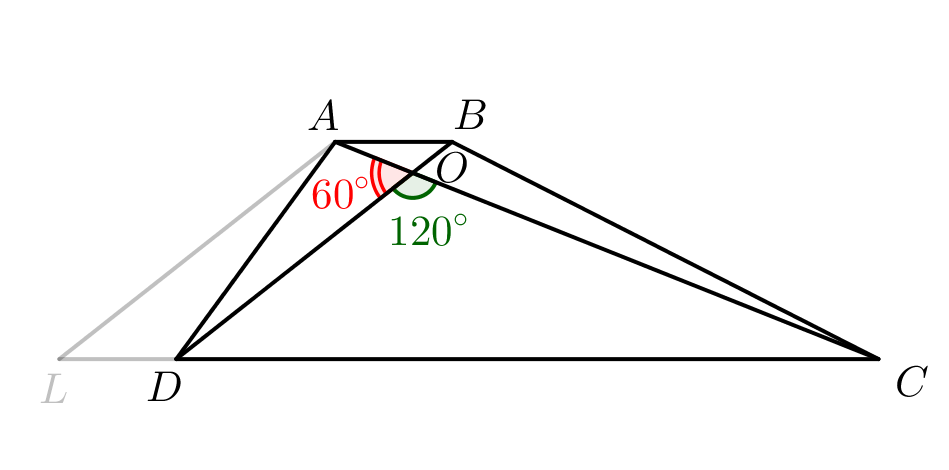 |
Ответ: \(\displaystyle 60^{\circ}\small.\)