На рисунке обозначены два равных отрезка и два равных угла.
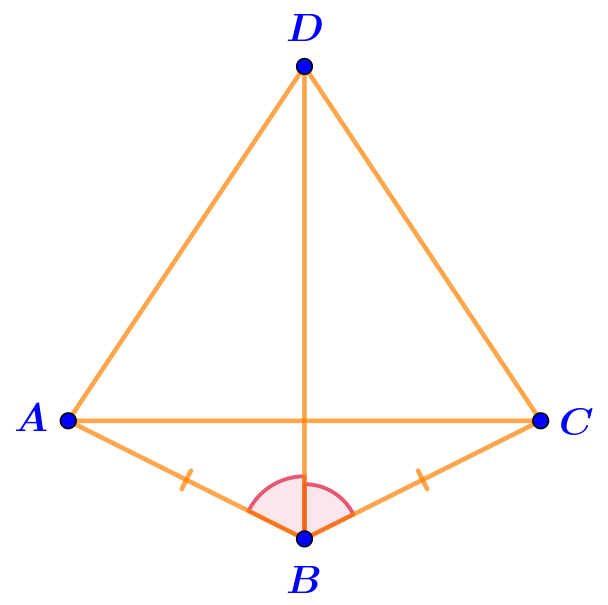
Дополните доказательство равенства углов \(\displaystyle DAC\) и \(\displaystyle DCA{\small .}\)
\(\displaystyle 1.\; \left\{ \begin{array}{ll} \\\\\\\\\\ \end{array} \right.\) | \(\displaystyle {\LARGE\Rightarrow}\) | \(\displaystyle {\LARGE\Rightarrow}\) | |||
| \(\displaystyle BD -\text{ \footnotesize\itобщая сторона}\) | \(\displaystyle {\bf\triangle}ABD={\bf\triangle}CBD\) | \(\displaystyle AD=DC\) | |||
\(\displaystyle \text{ \footnotesize\it(по первому признаку)}\) |
|
| \(\displaystyle 2.\) | \(\displaystyle {\LARGE\Rightarrow}\) | \(\displaystyle \angle DAC=\angle DCA\) | |
| \(\displaystyle \text{ \footnotesize\it(углы при основании равнобедренного треугольника)}\) |
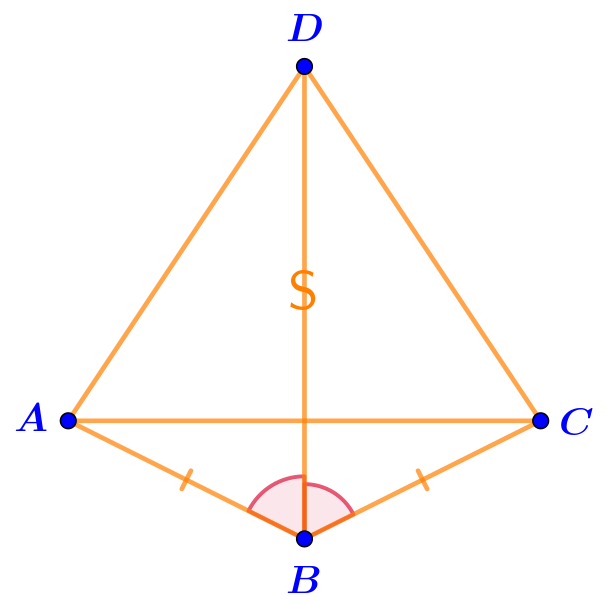
\(\displaystyle \left\{\begin{array}{ll}BA=BC\\BD -\text{ \footnotesize\itобщая сторона}\\\angle ABD=\angle CBD\end{array}\quad{\LARGE\Rightarrow}\,\begin{array}{c} \\{\bf\triangle}ABD={\bf\triangle}CBD\\\text{ \footnotesize\it(по первому признаку)}\end{array}\right.\)
Значит,
\(\displaystyle AD=DC{\small .}\)
Треугольник \(\displaystyle ADC\,-\) равнобедренный треугольник по определению.
По свойству равнобедренного треугольника, углы при основании \(\displaystyle AC\) равны.
Оформляя это в виде записи, получаем:
\(\displaystyle AD=DC\quad{\LARGE\Rightarrow}\quad\angle DAC=\angle DCA\text{ \footnotesize\it (по свойству углов равнобедренного треугольника)}{\small .}\)
Можно использовать запись:
\(\displaystyle \triangle ADC \text{ \footnotesize\it равнобедроенный}\quad{\LARGE\Rightarrow}\quad\angle DAC=\angle DCA\text{ \footnotesize\it (по свойству углов равнобедренного треугольника)}{\small .}\)
Но это хуже. При такой записи неясно, какая из сторон является основанием и какие углы \(\displaystyle -\) равными.
