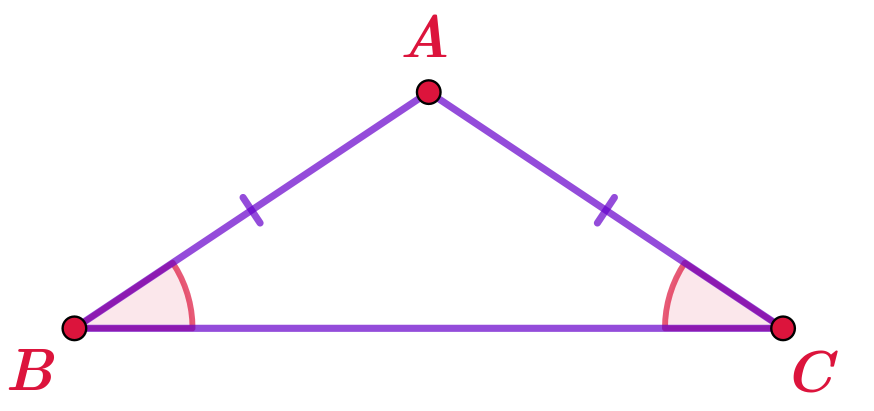
В треугольнике \(\displaystyle ABC\) отмечены равные стороны.
Известно, что \(\displaystyle \angle CAB+\angle CBA=42\degree {\small .}\)
Найти величину угла \(\displaystyle CAB{\small .}\)
\(\displaystyle \angle CAB=\)\(\displaystyle \degree \)
В равнобедренном треугольнике \(\displaystyle ABC\) углы при основании \(\displaystyle AB\) равны:
\(\displaystyle \angle CAB=\angle CBA{\small .}\)
Отметим это на рисунке:
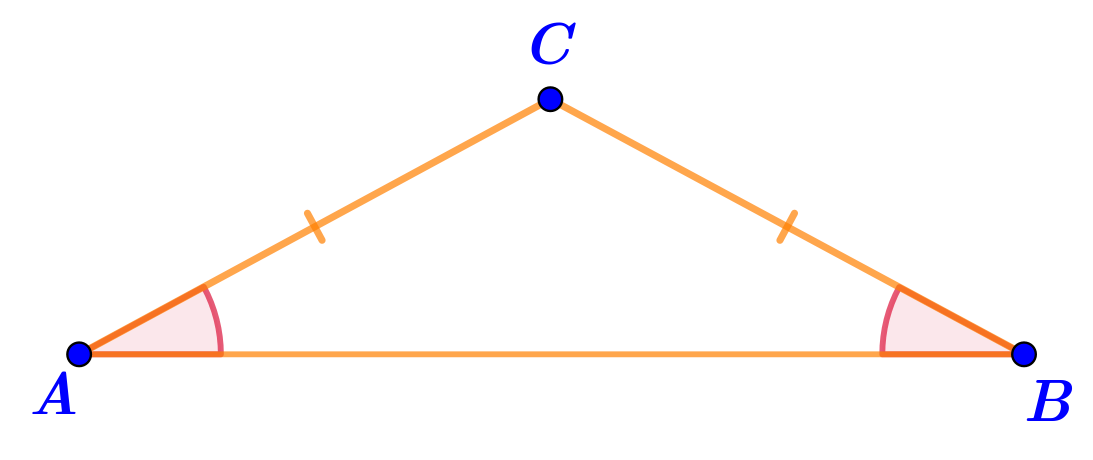
Сумма величин двух этих равных углов по условию равна \(\displaystyle 42\degree {\small :}\)
\(\displaystyle \angle CAB+\angle CBA=42\degree {\small .}\)
Чтобы найти величину искомого угла, нужно разделить это число на два:
\(\displaystyle \angle CAB=\frac{42\degree}{2}=21\degree{\small .}\)
Ответ:\(\displaystyle \angle CAB=21\degree{\small .}\)