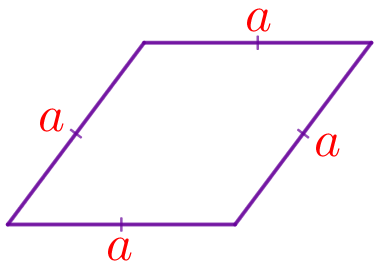
Задание
Найдите периметр ромба \(\displaystyle ABCD{\small,}\) в котором \(\displaystyle AB=20\, {\footnotesize см}{\small.}\)
\(\displaystyle P_{ABCD}=\) \(\displaystyle {\footnotesize см}{\small.}\)
Решение
Определение
| Ромбом называется параллелограмм, у которого все стороны равны. | 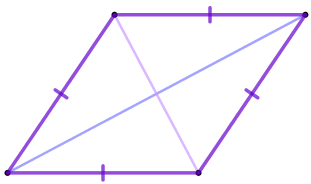 |
Требуется найти периметр данного ромба. | 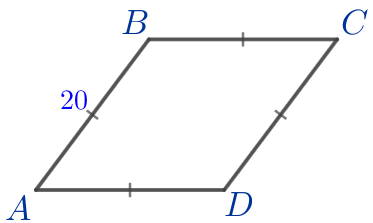 |
Периметр многоугольника равен сумме длин всех его сторон.
Периметр ромба \(\displaystyle ABCD\) можно вычислить по формуле
\(\displaystyle P_{ABCD}=4 \cdot AB{\small.}\)
Подставим \(\displaystyle AB=20\) в формулу периметра:
\(\displaystyle P_{ABCD}=4 \cdot AB{\small;}\)
\(\displaystyle P_{ABCD}=4 \cdot 20=80\, \footnotesize см{\small.}\)
Ответ: \(\displaystyle P_{ABCD}=80\, \footnotesize см{\small.}\)