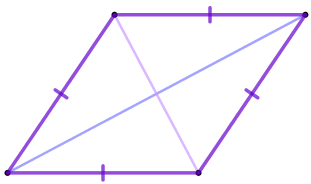
Сторона ромба \(\displaystyle ABCD\) равна \(\displaystyle 6 {\small,}\) угол между диагональю \(\displaystyle BD\) и стороной ромба равен \(\displaystyle 60^{\circ}{\small.}\) Найдите длину диагонали \(\displaystyle BD{\small.}\)
\(\displaystyle BD=\)
Требуется найти длину диагонали \(\displaystyle BD{\small.}\) | 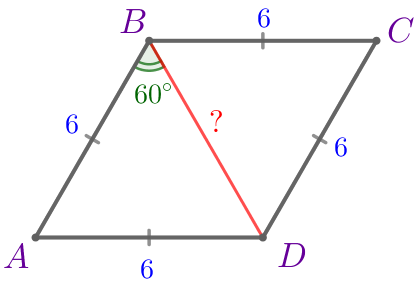 |
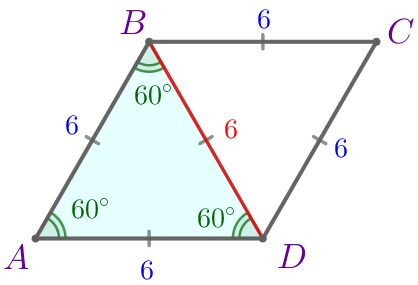
Рассмотрим треугольник \(\displaystyle ABD{\small.}\)
| \(\displaystyle AB=AD\) – по определению ромба. Значит, \(\displaystyle \triangle ABD\) – равнобедренный. |
В равнобедренном треугольнике углы при основании равны:
\(\displaystyle \angle ADB = \angle ABD = 60^{\circ}{\small.}\)
Поскольку сумма углов треугольника составляет \(\displaystyle 180^{\circ}{\small,}\) то
\(\displaystyle \angle BAD = 180^{\circ}-\angle ABD - \angle ADB = 180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}{\small.}\)
Так как три угла треугольника \(\displaystyle ABD\) равны по \(\displaystyle 60^{\circ}{\small,}\) то \(\displaystyle \triangle ABD\) – равносторонний, то есть
\(\displaystyle BD=AB=AD=6{\small.}\)
Длина диагонали \(\displaystyle BD\) равна \(\displaystyle 6{\small.}\)
Ответ: \(\displaystyle 6 {\small .}\)