В прямоугольнике \(\displaystyle ABCD\) диагонали пересекаются в точке \(\displaystyle O{\small.}\) Найдите периметр треугольника \(\displaystyle AOB{\small,}\) если \(\displaystyle \angle CAD=30^{\circ}{\small,}\) \(\displaystyle AC=12\, {\footnotesize см}{\small.}\)
\(\displaystyle P_{AOB}=\) \(\displaystyle {\footnotesize см}{\small.}\)
| 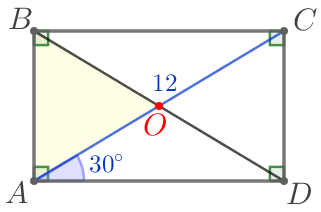 |
Требуется найти периметр треугольника \(\displaystyle AOB{\small:}\)
\(\displaystyle P_{\triangle AOB}=AB+OA+OB=\color{red}{\Large?}\)
Найдём длины отрезков \(\displaystyle OA{\small,}\) \(\displaystyle OB{\small,}\) \(\displaystyle AB{\small.}\)
\(\displaystyle BD=AC=12\, {\footnotesize см}{\small;}\)
\(\displaystyle OA=OB=OC=OD{\small.}\)
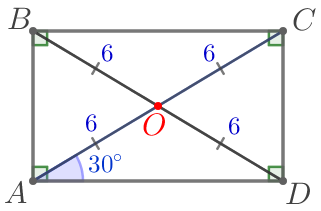 | \(\displaystyle OA=OB=12:2=6\, {\footnotesize см}{\small.}\) |
Рассмотрим равнобедренный треугольник \(\displaystyle AOB{\small.}\)
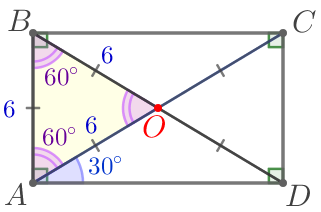 | Угол \(\displaystyle OAB\) равен разности углов \(\displaystyle BAD\) и \(\displaystyle OAD{\small:}\) \(\displaystyle \angle OAB=90^{\circ}-30^{\circ}=60^{\circ}{\small.}\) В равнобедренном треугольнике углы при основании равны, значит, \(\displaystyle \angle OBA=\angle OAB=60^{\circ}{\small.}\) |
\(\displaystyle \triangle AOB\) – равносторонний
\(\displaystyle AB=OA=OB=6\, {\footnotesize см}{\small.}\)
Найдём периметр треугольника \(\displaystyle AOB{\small:}\)
\(\displaystyle P_{\triangle AOB}=AB+OA+OB=6+6+6=18\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle P_{\triangle AOB}=18\, {\footnotesize см}{\small.}\)