В прямоугольнике \(\displaystyle ABCD\) \(\displaystyle AB=19\, {\footnotesize см}{\small,}\) \(\displaystyle AD=12\, {\footnotesize см}{\small.}\) Биссектриса угла \(\displaystyle A\) пересекает сторону \(\displaystyle CD\) в точке \(\displaystyle K{\small.}\) Найдите длину отрезка \(\displaystyle CK{\small.}\)
\(\displaystyle CK=\) \(\displaystyle {\footnotesize см}{\small.}\)
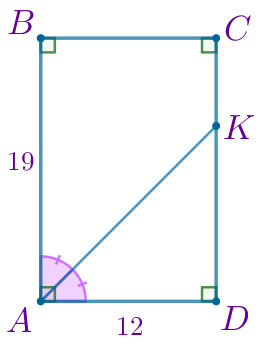
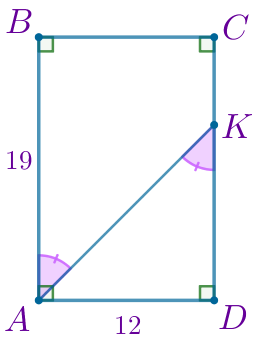
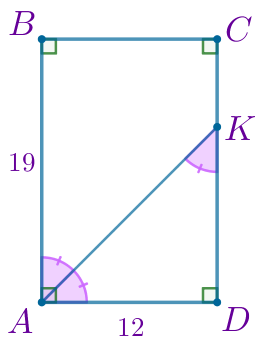
По условию задачи выполним построение.
Требуется найти длину отрезка \(\displaystyle CK{\small.}\) | 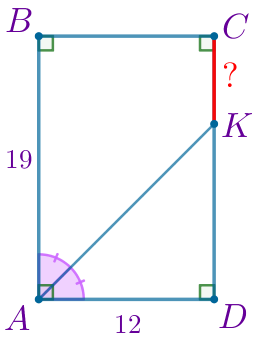 |
Так как точка \(\displaystyle K\) лежит на стороне \(\displaystyle CD{\small,}\) то
\(\displaystyle CK=CD-KD{\small.}\)
Найдём длины отрезков \(\displaystyle CD\) и \(\displaystyle KD{\small:}\)
\(\displaystyle CD=19\, {\footnotesize см}{\small.}\)
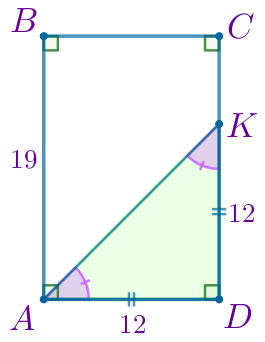
\(\displaystyle KD=12\, {\footnotesize см}{\small.}\)
Найдём длину отрезка \(\displaystyle CK{\small:}\)
\(\displaystyle CK=CD-KD{\small;}\)
\(\displaystyle CK=19-12=7\, {\footnotesize см}{\small.} \)
Ответ: \(\displaystyle CK=7\, {\footnotesize см}{\small.} \)