Длина стороны клетки равна \(\displaystyle 1\)см. Найдите длину отрезка \(\displaystyle PC\small.\)
Теорема об отрезках секущих
Если две секущие проходят через одну точку, то произведение отрезков одной секущей равно произведению отрезков другой секущей:
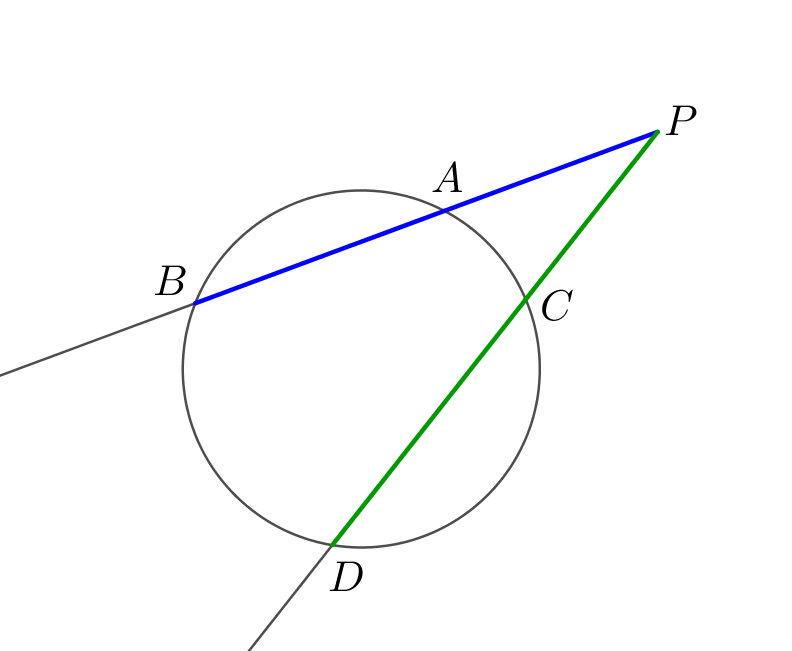
\(\displaystyle \color{blue}{AP}\cdot \color{blue}{BP}=\color{green}{CP}\cdot \color{green}{ DP}\)
Тогда получаем:
\(\displaystyle AP\cdot BP=CP\cdot DP\small.\)
Чтобы найти \(\displaystyle CP\small,\) найдем \(\displaystyle AP,\,BP\) и \(\displaystyle DP\small.\)
Длина стороны клетки равна \(\displaystyle 1\)см, тогда
\(\displaystyle AP=2\)см и \(\displaystyle BP=8\)см.
Построим прямоугольный треугольник с гипотенузой \(\displaystyle DP\) и катетами, проходящими по линиям сетки. Катеты этого прямоугольного треугольника равны \(\displaystyle 3\)см и \(\displaystyle 5\)см. Тогда по теореме Пифагора: \(\displaystyle DP^2=3^2+5^2=34\small,\) \(\displaystyle DP=\sqrt{34}\)см. |
Подставим полученные значения:
\(\displaystyle 2\cdot 8=CP\cdot\sqrt{34}\small.\)
Находим \(\displaystyle CP{\small:}\)
\(\displaystyle CP=\frac{2\cdot 8}{\sqrt{34}}=\frac{16}{\sqrt{34}}=\frac{8\sqrt{34}}{17}\)см.
Ответ: \(\displaystyle CP=\frac{8\sqrt{34}}{17}\)см.