В параллелограмме \(\displaystyle ABCD\) провели диагональ \(\displaystyle BD{\small.}\) Площадь треугольника \(\displaystyle ABD\) равна \(\displaystyle 8\, {\footnotesize см^{2}}{\small.}\) Найдите площадь треугольника \(\displaystyle BCD{\small.}\)
\(\displaystyle S_{\triangle BCD}=\)\(\displaystyle {\footnotesize см^{2}}{\small.}\)
Рассмотрим треугольники \(\displaystyle ABD\) и \(\displaystyle BCD{\small.}\)
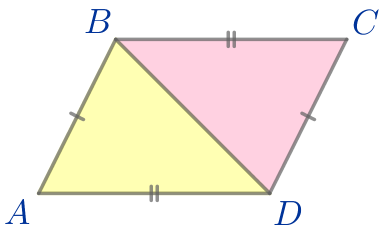 |
\(\displaystyle AB=CD{\small;}\) \(\displaystyle AD=BC{\small.}\)
|
Следовательно,
\(\displaystyle \triangle ABD= \triangle BCD\) по трем сторонам.
Равные многоугольники имеют равные площади.
Значит,
\(\displaystyle S_{\triangle BCD}=S_{\triangle ABD}=8\, {\footnotesize см^{2}}{\small.}\)
Ответ: \(\displaystyle S_{\triangle BCD}=8\, {\footnotesize см^{2}}{\small.}\)